Question

If two lines intersect, prove that the vertically opposite angles are equal.

Answer 1

Hint: We will suppose two lines AB and CD intersecting at point O and then we will use the linear pair Axiom which says that if a ray stands on a line, then the adjacent angle form a linear pair of angles mean their sum is equal to \[{{180}^{\circ }}\].

Complete step-by-step answer:
We have been asked to prove that the vertically opposite angles are equal if two lines intersect each other. Let us suppose two lines to be \[\overleftrightarrow{AB}\] and \[\overleftrightarrow{CD}\] intersecting at O. So, we have to prove \[\angle BOC=\angle AOD\] and \[\angle AOC=\angle BOD\].

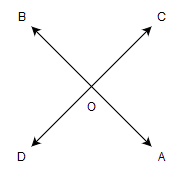
We can see in the figure that a ray \[\overrightarrow{OA}\] stands on the line \[\overleftrightarrow{CD}\] and according to linear pair Axiom, if a ray stands on a line, then the adjacent angles form a linear pair of angles.
\[\Rightarrow \angle AOD+\angle AOC=180......(1)\]
Again, the ray \[\overrightarrow{OC}\] stand on the line AB
According to linear pair Axiom, we have,
\[\Rightarrow \angle AOC+\angle BOC=180......(2)\]
Again, the ray \[\overrightarrow{OB}\] stand on the line CD
According to linear pair Axiom, we have,
\[\Rightarrow \angle BOC+\angle BOD=180......(3)\]
Also, the ray \[\overrightarrow{OD}\] stand on the line AB
According to linear pair axiom we have,
\[\Rightarrow \angle BOD+\angle AOD=180......(4)\]
Now on comparing equation (1) and (2) observe that their right hand side value are equal so their left hand value must be the same.
\[\begin{align}
  & \Rightarrow \angle AOD+\angle AOC=\angle AOC+\angle BOC \\
 & \Rightarrow \angle AOD=\angle BOC \\
\end{align}\]
These are vertically opposite angles.
Similarly, on comparing equation (3) and (4) we get as follows:
\[\begin{align}
  & \Rightarrow \angle BOC+\angle BOD=\angle BOD+\angle AOD \\
 & \Rightarrow \angle BOC=\angle AOD \\
\end{align}\]
These are also vertically opposite angles.
Therefore, it is proved that if two lines intersect then the vertically opposite angles are equal.

Note: Be careful while using the linear pair Axiom and making the equations and remember that according to linear pair Axiom if a ray stand on a line, then the adjacent angles form a linear pair or angle means their sum is equal to \[{{180}^{\circ }}\].