
If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, then prove that the chords are equal.

Answer
585.9k+ views
Hint: Here, we can use the AAS congruence criteria and prove that OL=OM. So, two chords will be equal using the property that chords are equal if they are equidistant from the centre of the circle.
Complete step-by-step solution -
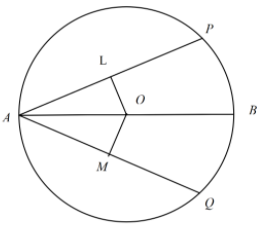
In the question, we have been given with the figure where O is the centre of the circle, as shown below:
And we have to prove that, chord AP=AQ.
It is given that two intersecting chords (AP and AQ) of a circle make equal angles with the diameter passing through their point of intersection A, therefore\[\angle PAB=\angle QAB\].
Also, we can say that \[\angle LAO=\angle MAO\]. Now, in the triangles \[\Delta \,AOL,\,\,\,\Delta \,AOM\]we have:
\[\angle LAO=\angle MAO\]
\[\angle ALO=\angle AMO={{90}^{\circ }}\]
AO= AO (common side)
So, using the AAS congruence criteria, we can say that \[\Delta \,AOL\cong \,\,\Delta \,AOM\]. Thus the two triangles \[\Delta \,AOL\,\,\text{ }\!\!\And\!\!\text{ }\,\,\,\Delta \,AOM\] are congruent. Hence, we can say that OL=OM.
Now, since OL and OM are the perpendicular distance of the two chords AP and AQ respectively. Also, we know that if two chords are equidistant from the centre of the circle then the two chords are equal. So, have the two chords AP and AQ equal, since they are equidistant from the centre of the circle. Hence proved.
Note: Here we cannot use the RHS congruence criteria, as it can be used only when two right angled triangles have same hypotenuse length and one other side of same length, in this case, there is no other side of same length.
Complete step-by-step solution -
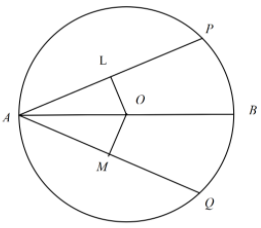
In the question, we have been given with the figure where O is the centre of the circle, as shown below:

And we have to prove that, chord AP=AQ.
It is given that two intersecting chords (AP and AQ) of a circle make equal angles with the diameter passing through their point of intersection A, therefore\[\angle PAB=\angle QAB\].
Also, we can say that \[\angle LAO=\angle MAO\]. Now, in the triangles \[\Delta \,AOL,\,\,\,\Delta \,AOM\]we have:
\[\angle LAO=\angle MAO\]
\[\angle ALO=\angle AMO={{90}^{\circ }}\]
AO= AO (common side)
So, using the AAS congruence criteria, we can say that \[\Delta \,AOL\cong \,\,\Delta \,AOM\]. Thus the two triangles \[\Delta \,AOL\,\,\text{ }\!\!\And\!\!\text{ }\,\,\,\Delta \,AOM\] are congruent. Hence, we can say that OL=OM.
Now, since OL and OM are the perpendicular distance of the two chords AP and AQ respectively. Also, we know that if two chords are equidistant from the centre of the circle then the two chords are equal. So, have the two chords AP and AQ equal, since they are equidistant from the centre of the circle. Hence proved.
Note: Here we cannot use the RHS congruence criteria, as it can be used only when two right angled triangles have same hypotenuse length and one other side of same length, in this case, there is no other side of same length.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




