Question

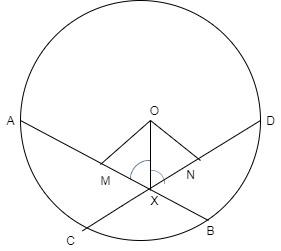
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
                                               

Answer 1

Hint – We will start solving this question by writing down the given things and what to prove and then we write the proof in which we will use different congruence rules.

Complete Step-by-Step solution:
First we will make the diagram and we will denote the angles to prove as $\angle 1$ and $\angle 2$.

                                                    

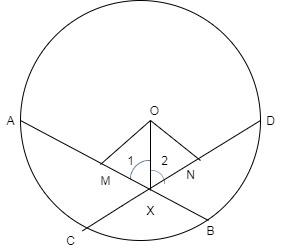
Given: The chord AB and CD are equal, i.e., AB = CD.

To prove: $\angle 1 = \angle 2$

Proof: In $\vartriangle OMX$and $\vartriangle ONX$, we have
$OX = OX$ - (Common)
$\angle M = \angle N$ - (Each $90^\circ $)
$OM = ON$ - (Equal chords are equidistant from each other)

$\therefore \vartriangle OMX \cong \vartriangle ONX$ - (By RHS rule)
Thus, $\angle 1 = \angle 2$ - (By CPCT)
Hence proved.

Note – A chord of a circle is a straight line segment whose endpoints both lie on the circle. For solving this question one should know all the rules of congruence because this is the one and only method to solve this question.