Question

If two cubical dice are thrown simultaneously, then find the probability of getting the sum of numbers ‘more than 7’ or ‘less than 7’.

Answer 1

Hint: Find out total number of outcomes when two dice are thrown simultaneously. Then find the total number of events in which the sum of the numbers on two dice is ‘more than 7’ and ‘less than 7’. Divide the number of desirable outcomes with the total number of outcomes to find the probability of both the cases.

Complete step-by-step answer:
Since, a cubical dice has six faces and each face has a number that range from 1 to 6. So, the total number of outcomes when 1 dice is thrown is 6. Therefore, when two dice are thrown, the total number of outcomes will be the total combinations of the 6 numbers of one die with the 6 numbers of the other die.

Now, let us come to the question.

Total number of outcomes or total number of sample space $=n(S)=6\times 6=36$

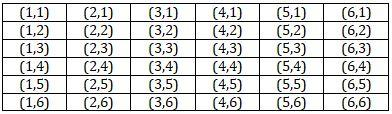
Combinations in which sum is more than 7 are: (2, 6); (3, 5); (3, 6); (4, 4); (4, 5); (4, 6); (5, 3); (5, 4); (5, 5); (5, 6); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6).

Therefore, the total number of outcomes in which sum is more than 7 $=n({{E}_{1}})$$=15$.

Combinations in which sum is less than 7 are: (1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (2, 1); (2, 2);
(2, 3); (2, 4); (3, 1); (3, 2); (3, 3); (4, 1); (4, 2); (4, 3).

Therefore, the total number of outcomes in which sum is less than 7 $=n({{E}_{2}})$$=15$.

We know that, probability of an event $=\dfrac{\text{number of desired
outcome}}{\text{total number of outcome}}=\dfrac{n(E)}{n(S)}$.

Therefore, probability of getting the sum more than 7
$=\dfrac{n({{E}_{1}})}{n(S)}=\dfrac{15}{36}=\dfrac{5}{12}$.

Also, probability of getting the sum less than 7
$=\dfrac{n({{E}_{2}})}{n(S)}=\dfrac{15}{36}=\dfrac{5}{12}$.


Note: It would be favourable for us to note all the outcomes in a table otherwise we may get confused in counting the desirable number of events. It is important to note that if ‘n’ number of dice is rolled simultaneously then the total number of outcomes will be ${{6}^{n}}$.