Question

If two circles touch each other extremely, prove that the centres and the point of contact are collinear.

Answer 1

Hint: We will be using the concepts of circle to solve the question, we will also be using concepts like tangent of a circle also we will be using the property of a straight line to further simplify the solution.

Step-by-step answer:
We have been given two circles which are touching each other externally. So let us first draw two circles of arbitrary radius which touch each other externally.

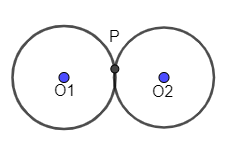
The two circles at centre $O_1$ and $O_2$ touch each other externally at P.
Now we will draw a common tangent to both the circles by passing through P.

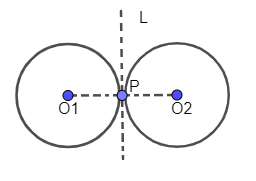
Now, we have to prove that $O_1$, P, $O_2$ are collinear or we can prove that ${{O}_{1}}P{{O}_{2}}$ is a straight line.
Now, we know that tangent makes an angle of $90{}^\circ $ with radius therefore
$\angle {{O}_{1}}PL=\dfrac{\pi }{2}$ ……………………..(1)
$\angle {{O}_{2}}PL=\dfrac{\pi }{2}$ …………………….(2)
 Now we will add (1) and (2)
$\angle {{O}_{1}}PL+\angle {{O}_{2}}PL=\dfrac{\pi }{2}+\dfrac{\pi }{2}$
$\angle {{O}_{1}}P{{O}_{2}}=\pi $
Since $\angle {{O}_{1}}P{{O}_{2}}=\pi $ this means that the line ${{O}_{1}}P{{O}_{2}}$ is a straight line. Hence $O_1$, P, $O_2$ are collinear.

Note: To solve this type of question one must know that the tangent makes an angle of $90{}^\circ $ with the radii also angle in a straight line is $180{}^\circ $ this helps in simplifying the problem.