Question

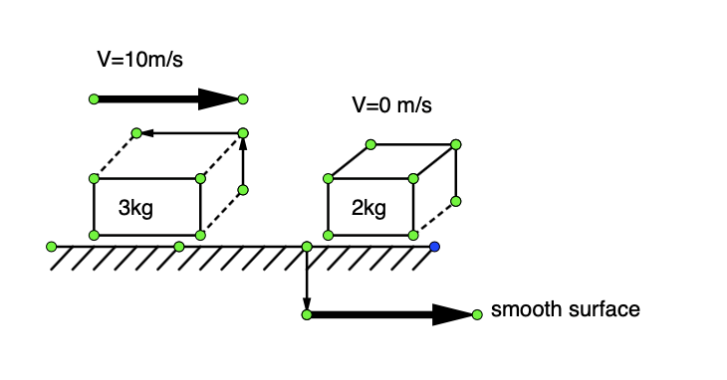
If the two blocks collide heat on and stick together, on a frictionless horizontal surface, then the interacting impulse between the two blocks is

Answer 1

Hint: We know that according to the law of conservation of energy “energy can neither be created nor destroyed it may transfer from one form to another and makes the total energy constant”.

Formula used: Change in momentum is given by $\overrightarrow J = F.dt = {P_f} - {P_i}$where ‘P’ is representing momentum which is equal to $m.v$, we will use this concept and law of conservation of energy to solve this question.

Complete step by step answer: It is given in the question that two blocks collide heat on and stick together, on a frictionless horizontal surface, then we have to find the interacting impulse between the two blocks. It is also shown in the diagram that blocks 1 is off $3kg$ and block 2 is off $2kg$ also, the initial velocity of blocks is $10m/s, 0m/s$ respectively.
${m_1} = 3kg$, the initial velocity of ${m_1}$ $ = $ $10m/s$
${m_2} = 2kg$, the initial velocity of ${m_2}$ $ = $ $0m/s$.

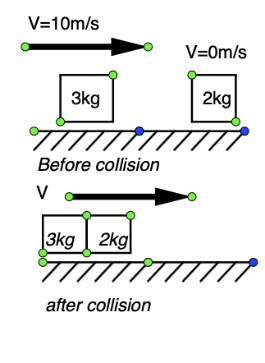
Now, we know that according to the law of conservation of energy “energy can neither be created nor destroyed it may transfer from one form to another and makes the total energy constant”. So, we will conserve the initial momentum and final momentum of the block 1 and block 2 we get-
${m_1}{v_1} + {m_2}{v_2} = ({m_1} + {m_2})v$
Here, v is the final velocity of both the block after the collision. On putting the vales, we get-
$3 \times 10 + 2 \times 0 = (3 + 2)v$
$30 + 0 = 5v$
$v = \dfrac{{30}}{5} = 6m/s$
So, the final velocity of both the block will be $6m/s$.
If we see the free body diagram of both the block during collision we get-

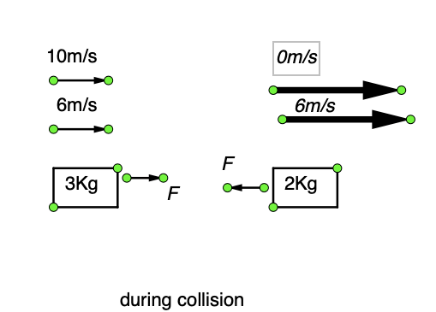
We know that impulse means the change in momentum of a body in a small interval of time. We can calculate the change in impulse $\overrightarrow J = F.dt = {P_f} - {P_i}$. Here, $\overrightarrow J $ is the change in impulse whereas ${P_f}$ is final momentum and ${P_i}$ is initial momentum. It is also noted that $momentum(P) = m.v$ where m is the mass of the body and v is the velocity of the body.
We will calculate the change in the momentum of both the bodies individually. Change in the momentum of block 1 is given by $\overrightarrow J = F.dt = {P_f} - {P_i}$. On putting values, we get –
$\overrightarrow J = 3 \times 6 - 3 \times 10$
\[\overrightarrow J = 18 - 30\]
$\overrightarrow J = - 12N/s$
Here, the negative sign represents the impulse in the opposite direction of the velocity.
Similarly, the change in momentum of block 2 is given by $\overrightarrow J = F.dt = {P_f} - {P_i}$. On putting values, we get-
$\overrightarrow J = 2 \times 6 - 2 \times 0$
\[\overrightarrow J = 12 - 0\]
$\overrightarrow J = 12N/s$
Therefore, the change in momentum of block 1 will be $\overrightarrow J = - 12N/s$and the change in momentum of block 2 will be $\overrightarrow J = 12N/s$.

Note: The momentum is defined as the ‘mass in motion’ or we can say that it is the product of mass and velocity. It is also noted that momentum is a vector quantity and it depends on the direction. For example, in the above the momentum of block 1 is $\overrightarrow J = - 12N/s$ and the momentum of block 2 is $\overrightarrow J = 12N/s$ both are different because both are in opposite directions. Its SI unit is N/s which is also equal to $kgm/s$.