Question

If the trigonometric angle is given by $15\cot A=8$, then find the value of $\sin A$ and $\sec A$.

Answer 1

Hint: We will apply the formula $\cot \left( A \right)=\dfrac{\text{Base}}{\text{Perpendicular}}$ to form the triangle and after that we will use the Pythagoras theorem to find the hypotenuse of the triangle in order to solve the question.

Complete step-by-step answer:
We will first consider here the expression given in the question as $15\cot A=8$. We will divide this equation by 15 on both the sides. Therefore, we get $\cot A=\dfrac{8}{15}$. Now we will apply the formula given by $\cot \left( A \right)=\dfrac{\text{Base}}{\text{Perpendicular}}$. Therefore by comparing $\cot A=\dfrac{8}{15}$ and $\cot \left( A \right)=\dfrac{\text{Base}}{\text{Perpendicular}}$ we get base of the triangle as 8 units and perpendicular as 15 units. The diagram showing this is given below.

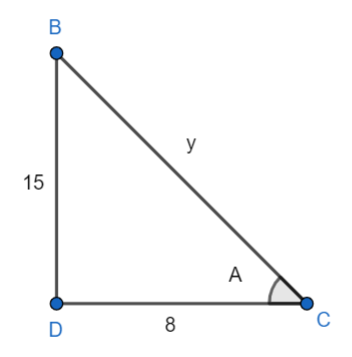
Now we will use Pythagoras theorem to this right angular triangle. Therefore, we have ${{y}^{2}}={{\left( 15 \right)}^{2}}+{{\left( 8 \right)}^{2}}$. Since, the square of 15 is 225 and the square of 8 is 64. Therefore, we get ${{y}^{2}}$ as 225 + 64. This results in ${{y}^{2}}$ as 289. And the square root of 289 is given by 17. Therefore, we get $y=\pm 17$. As we know that the side of the triangle cannot be negative. So, we have y = 17 units. And this represents the hypotenuse of the triangle.
Now, we will consider the term $\sin A$. So, By taking the same diagram as a guide, we can use the formula $\sin A=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. As we know that the perpendicular in the triangle is 15 units and the hypotenuse is 17 units. Therefore, we have $\sin A=\dfrac{15}{17}$.
Now, we will consider another trigonometric term $\sec A$. Here, we will take the same figure as a guide, so the formula of $\sec A=\dfrac{\text{Hypotenuse}}{\text{Base}}$. As we can clearly see in the diagram that the hypotenuse is 17 units and base is 8 units. Therefore, we have $\sec A=\dfrac{17}{8}$.

Note: Alternate method for solving this question is being done here. After finding the value of $\sin A=\dfrac{15}{17}$ we can use the formula given by ${{\sin }^{2}}\left( A \right)+{{\cos }^{2}}\left( A \right)=1$ or, ${{\cos }^{2}}\left( A \right)=1-{{\sin }^{2}}\left( A \right)$. Therefore, we get
$\begin{align}
  & {{\cos }^{2}}\left( A \right)=1-{{\left( \dfrac{15}{17} \right)}^{2}} \\
 & \Rightarrow {{\cos }^{2}}\left( A \right)=1-\dfrac{225}{289} \\
 & \Rightarrow {{\cos }^{2}}\left( A \right)=\dfrac{289-225}{289} \\
 & \Rightarrow {{\cos }^{2}}\left( A \right)=\dfrac{64}{289} \\
 & \Rightarrow \cos \left( A \right)=\pm \dfrac{8}{17} \\
\end{align}$
As we know that the side of the triangle cannot be negative so, we will have $\cos \left( A \right)=\dfrac{8}{17}$. Since, we can write $\cos \left( A \right)$ as $\dfrac{1}{\sec \left( A \right)}$. Therefore, we have
$\begin{align}
  & \cos \left( A \right)=\dfrac{8}{17} \\
 & \Rightarrow \dfrac{1}{\sec \left( A \right)}=\dfrac{8}{17} \\
 & \Rightarrow \sec \left( A \right)=\dfrac{17}{8} \\
\end{align}$