Question

If the tangents drawn at P (3,2$\sqrt{3}$ ) and Q (2, -2$\sqrt{2}$ ) to the parabola ${{y}^{2}}=4x$ intersects at T. Then find the co-ordinates of T and ar $\Delta $ PQT: ar $\Delta $ VPQ, where V is the vertex of the parabola.

Answer 1

Hint: In order to solve the above problem, first we will find tangent at P and Q and then solve these tangent equations to get the intersection point T. Then we will find the area of $\Delta $ PQT using determinant formula, that is suppose if the coordinates of vertex of a triangle is given as A , B $\left( {{x}_{2}},{{y}_{2}} \right)$ and C $\left( {{x}_{3}},{{y}_{3}} \right)$ then the area of triangle ABC using determinant formula is given by $\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|$. And then we will find the area of $\Delta $ VPQ using same determinant formula, where V is vertex of parabola. After that we will find the ratio of their areas and get the desired result.

Complete step by step answer:

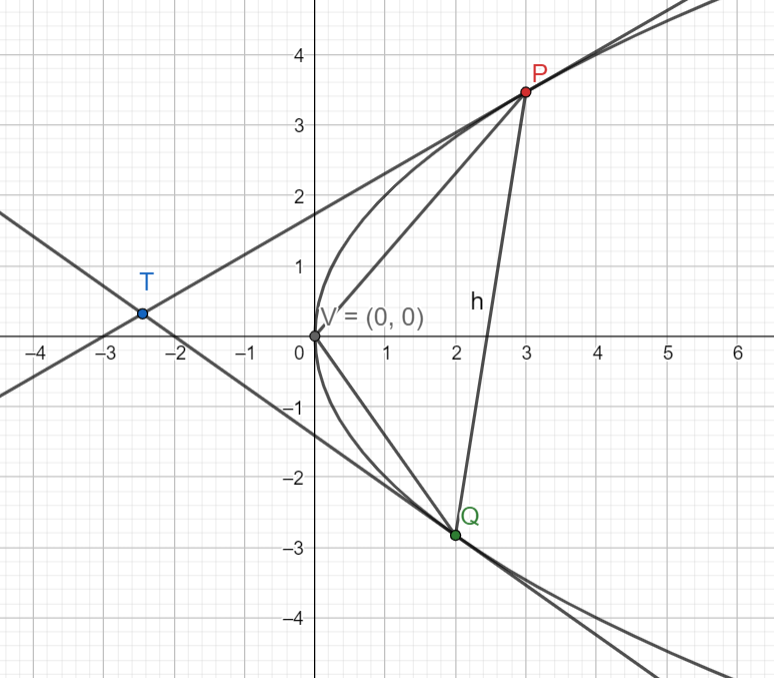
The equation of given parabola is ${{y}^{2}}=4x$
Generally, equation of tangent to a parabola ${{y}^{2}}=4ax$ at $({{x}_{1}},{{y}_{1}})$ is given by $y{{y}_{1}}-2a(x+{{x}_{1}})=0$ , so the equation of tangent to the parabola at point P (3,2$\sqrt{3}$ ) is given by $y(2\sqrt{3})-2(x+2)=0$ i.e. \[\sqrt{3}y-x-3=0\] .........(i)
and the equation of tangent to the parabola at Q (2, -2$\sqrt{2}$ ) is given by $y(-2\sqrt{2})-2(x+2)=0$ i.e. $\sqrt{2}y+x+2=0$ ...........(ii)
Adding equations (i) and (ii), we get
$\begin{align}
  & y(\sqrt{2}+\sqrt{3})-1=0 \\
 & \Rightarrow y=\dfrac{1}{\sqrt{2}+\sqrt{3}} \\
 & \Rightarrow y=\dfrac{1}{\sqrt{2}+\sqrt{3}}\times \dfrac{\sqrt{2}-\sqrt{3}}{\sqrt{2}-\sqrt{3}} \\
 & \Rightarrow y=\sqrt{2}-\sqrt{3} \\
\end{align}$
Putting ,the value of y in equation (i), we get
$\begin{align}
  & \sqrt{3}(\sqrt{3}-\sqrt{2})-x-3=0 \\
 & \Rightarrow x=-\sqrt{6} \\
\end{align}$
Therefore coordinate of T is $(-\sqrt{6},\sqrt{3}-\sqrt{2})$ .
Now, we have, P (3,2$\sqrt{3}$ ), Q (2, -2$\sqrt{2}$ ), T$(-\sqrt{6},\sqrt{3}-\sqrt{2})$,
$\therefore $ Area of $\Delta $ PQT =
$\dfrac{1}{2}\left| \begin{matrix}
   3 & 2\sqrt{3} & 1 \\
   2 & -2\sqrt{2} & 1 \\
   -\sqrt{6} & \sqrt{3}-\sqrt{2} & 1 \\
\end{matrix} \right|$
Applying row transformations on ${{R}_{1}}\text{ and }{{R}_{2}}$ that is ${{R}_{1}}\to {{R}_{1}}-{{R}_{3}}\text{ and }{{R}_{2}}\to {{R}_{2}}-{{R}_{3}}$ , we have
Area of $\Delta $ PQT =
$\dfrac{1}{2}\left| \begin{matrix}
   3+\sqrt{6} & \sqrt{3}+\sqrt{2} & 0 \\
   2+\sqrt{6} & -\sqrt{3}-\sqrt{2} & 0 \\
   -\sqrt{6} & \sqrt{3}-\sqrt{2} & 1 \\
\end{matrix} \right|$
Expanding the determinant along ${{C}_{3}}$ , we have
Area of $\Delta $ PQT
$\begin{align}
  & =\dfrac{1}{2}\left[ -\sqrt{3}\left( \sqrt{3}+\sqrt{2} \right)\left( \sqrt{3}+\sqrt{2} \right)-\sqrt{2}\left( \sqrt{3}+\sqrt{2} \right)\left( \sqrt{3}+\sqrt{2} \right) \right] \\
 & =\dfrac{1}{2}\left[ -{{\left( \sqrt{3}+\sqrt{2} \right)}^{2}}\left( \sqrt{3}+\sqrt{2} \right) \right] \\
 & ={{\dfrac{-\left( \sqrt{3}+\sqrt{2} \right)}{2}}^{3}} \\
\end{align}$
But since area is always positive, so taking modulus of area, we have
$\text{Area of }\Delta \text{PQT}=\left| \dfrac{-{{\left( \sqrt{3}+\sqrt{2} \right)}^{3}}}{2} \right|=\dfrac{{{\left( \sqrt{3}+\sqrt{2} \right)}^{3}}}{2}$
Similarly, we have P (3,2$\sqrt{3}$ ), Q (2, -2$\sqrt{2}$ ), V (0,0) ,
$\therefore $ Area of $\Delta $ VPQ $=\dfrac{1}{2}\left| \begin{matrix}
   0 & 0 & 1 \\
   2 & 2\sqrt{3} & 1 \\
   2 & -2\sqrt{2} & 1 \\
\end{matrix} \right|$
Expanding the determinant along ${{R}_{\,1}}$ , we have
Area of $\Delta $ VPQ
 \[\begin{align}
  & =\dfrac{1}{2}\left[ 1\left( -6\sqrt{2}-4\sqrt{3} \right) \right] \\
 & =\dfrac{1}{2}\left[ -2\sqrt{6}\left( \sqrt{3}+\sqrt{2} \right) \right] \\
 & =\dfrac{-2\sqrt{6}\left( \sqrt{3}+\sqrt{2} \right)}{2} \\
\end{align}\]
But since area is always positive taking modulus of area,we have
Area of $\Delta $ VPQ
\[=\left| \dfrac{-2\sqrt{6}\left( \sqrt{3}+\sqrt{2} \right)}{2} \right|=\dfrac{2\sqrt{6}\left( \sqrt{3}+\sqrt{2} \right)}{2}\]

Now, ar $\Delta $ PQT: ar $\Delta $ VPQ
$\begin{align}
  & =\dfrac{\text{area of }\Delta \text{PQT}}{\text{area of }\Delta \text{VPQ}} \\
 & =\dfrac{\dfrac{{{\left( \sqrt{3}+\sqrt{2} \right)}^{3}}}{2}}{\dfrac{2\sqrt{6}\left( \sqrt{3}+\sqrt{2} \right)}{2}} \\
 & =\dfrac{{{\left( \sqrt{3}+\sqrt{2} \right)}^{2}}}{2\sqrt{6}} \\
 & =\dfrac{3+2+2\sqrt{6}}{2\sqrt{6}} \\
 & =\dfrac{5}{2\sqrt{6}}+1=\dfrac{5}{2\sqrt{6}}\times \dfrac{\sqrt{6}}{\sqrt{6}}+1=\dfrac{5\sqrt{6}}{12}+1 \\
\end{align}$
$\therefore $ ar $\Delta $ PQT: ar $\Delta $ VPQ = $5\sqrt{6}+12:12$

Note:
 Here in this problem, while calculating the area of $\Delta $ PQT , direct expansion of the determinant becomes complex, so in order to avoid this try to use the property of determinant as used above in the solution to make calculations easier.