Question

If the sum of the opposite angles of a quadrilateral is \[{180^0}\], the quadrilateral is cyclic.

Answer 1

Hint: Cyclic Quadrilateral is a quadrilateral if all four vertices lie on the circle circumference. We prove this statement by assuming a point out of the circle which is collinear to two vertices of the quadrilateral and using the exterior angle property we prove that the point outside the circle coincides with the vertex of the quadrilateral.

Complete step-by-step answer:
          

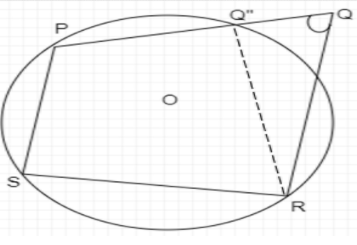
We assume the quadrilateral PQRS has sum of opposite angles \[{180^ \circ }\]
\[\angle PSR + \angle PQR = {180^ \circ }\]
\[\angle SRQ + \angle SPQ = {180^ \circ }\]
We know there are three non-collinear points P, S, and R. We know a circle with centre O passes through three collinear points, so we assume point Q does not lie on Circle, so three collinear points are P, Q” and Q.

PQ”RS is a cyclic quadrilateral as all the vertices of the quadrilateral lie on the circle. We know that for a cyclic quadrilateral sum of opposite angles is ${180^ \circ }$. That is

\[\angle PSR + \angle PQ''R = {180^ \circ }\] … (1)

But it is given

\[\angle PSR + \angle PQR = {180^ \circ }\] … (2)

So by comparing (1) and (2) we can write

\[\angle PSR + \angle PQR = \angle PSR + \angle PQ''R\]
\[\angle PSR - \angle PSR + \angle PQR = \angle PQ''R\]
\[\angle PQR = \angle PQ''R\] … (3)

In triangle RQQ”, from exterior angle property which states that the exterior of the triangle is equal to the sum of opposite angles of the triangle.

\[\angle PQ''R = \angle Q''QR + \angle Q''RQ\] … (4)

Using Equation (3) in Equation (4)

\[\angle PQR = \angle Q''QR + \angle Q''RQ\]

We can see from the diagram that

\[
  \angle PQR = \angle PQR + \angle Q''RQ \\
  \angle PQR - \angle PQR = \angle Q''RQ \\
  0 = \angle Q''RQ \\
 \]

This can be only true if, Q and Q” coincides. Therefore Point Q should lie on the circle.
Hence it is proved that if the sum of the opposite angles of a quadrilateral is \[{180^ \circ }\] , the quadrilateral is cyclic.

Note: Students can get confused with the diagram, and they might assume the angle Q” as right angle but keep in mind unless you are given from the diagram or separately, don’t assume any angle on your own.