Question

If the sides of the triangle are 17, 25 and 28, then find the greatest length of the altitude.

Answer 1

Hint: We will first draw the figure from the details given in the question then we will find the area of the triangle using base and height. Then we will find the area of the triangle using heron’s formula \[{{A}^{2}}=s(s-a)(s-b)(s-c).......(4)\] and then we will substitute this area to find the altitude.

Complete step-by-step answer:
We will first draw the figure from the details given in the question.

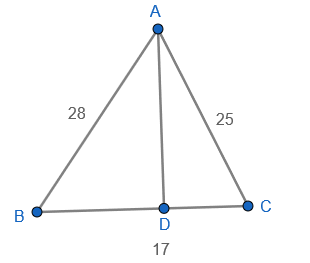
So from the figure we can clearly see that the greatest altitude AD is perpendicular to the shortest side BC.
Also AB is 28, AC is 25 and BC is 17.
Now we know that the area of the triangle is half into the base into the height. So using this information we get,
\[A=\dfrac{1}{2}\times base\times height......(1)\]
Now from the figure we can see that base is BC and height is AD. So substituting these in equation (2) we get,
\[A=\dfrac{1}{2}\times BC\times AD......(2)\]
Now substituting the value of BC and isolating AD by rearranging in equation (2) we get,
\[AD=\dfrac{2A}{17}......(3)\]
Now we also know that the area of triangle when length of three sides is known is,
\[{{A}^{2}}=s(s-a)(s-b)(s-c).......(4)\] where \[s=\dfrac{a+b+c}{2}\] and a is AB, AC is b and BC is c.
So \[s=\dfrac{28+25+17}{2}=\dfrac{70}{2}=35\] and hence substituting all the values in equation (4) we get,
\[\begin{align}
  & {{A}^{2}}=35(35-28)(35-25)(35-17) \\
 & {{A}^{2}}=35\times 7\times 10\times 18=44100......(5) \\
\end{align}\]
Now taking the square root of both the sides of the equation (5) we get,
\[A=\sqrt{44100}=210......(6)\]
Now substituting the value of A from equation (6) in equation (3) we get,
\[AD=\dfrac{2\times 210}{17}......(7)\]
Now solving equation (7) we get,
\[AD=\dfrac{420}{17}\]
Hence the greatest length of altitude is \[\dfrac{420}{17}\].

Note: Drawing the figure in these types of questions is the key and also remembering the different formulas of the area of the triangle is important. We in a hurry can make a mistake in solving equation (5) by substituting \[s=\dfrac{a+b+c}{3}\] instead of \[s=\dfrac{a+b+c}{2}\] and hence we need to be careful while doing this step.