Question

If the sides be 18, 24, 30cms, then radius of in-circle is
A. 2
B. 4
C. 6
D. 9

Answer 1

Hint: Find the area of triangle to find the radius of incircle using the formula,
Area= $\dfrac{1}{2}\times \text{base}\times \text{height}$

Complete step-by-step answer:

The sides of the triangle given in the question are 18cm, 24cm, 30cm.

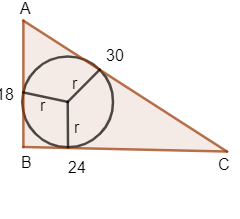
Let AB be 18cm, BC be 24cm and AC be 30cm.

$A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$

$\Rightarrow {{18}^{2}}+{{24}^{2}}={{30}^{2}}$

$\begin{align}

  & \Rightarrow 324+579={{30}^{2}} \\

 & \Rightarrow 900=900 \\

\end{align}$

Thus the sides of $\Delta $ ABC satisfy Pythagora's theorem.
Hence ABC is a right angled triangle.
Let ABC be a triangle with AB=18cm, BC=24cm and AC=30cm and a circle is inserted in triangle with radius ‘r’.
Let O be the centre of the circle.
Area of $\Delta $ ABC = Area of AOB + Area of BOC + Area of COA…….. (1)
Area of right angled triangle = $\dfrac{1}{2}\times \text{base}\times \text{height}$
Substituting the corresponding values, we get
Area of $\Delta $ ABC $=\dfrac{1}{2}\times 18\times 24=216$
Area of $\Delta $ AOB =$\dfrac{1}{2}\times r\times 18=9r$
Area of $\Delta $ BOC =$\dfrac{1}{2}\times r\times 24=12r$
Area of $\Delta $ COA =$\dfrac{1}{2}\times r\times 30=15r$
So, putting back the values in the equation (1) we get,
$\begin{align}
  & 216=9r+12r+15r \\
 & \Rightarrow 36r=216 \\
 & \Rightarrow r=6 \\
\end{align}$
So, the answer is C.

Note: There is a shortcut to solve this problem using the formula, radius = $\left( \dfrac{a+b-c}{2} \right)$ if a, b are the sides and c is the hypotenuse of the triangle. This shortcut can be used only when the triangle is a right angled triangle.