Question

If the ratio of maximum and minimum intensities in an interference pattern is $36:1$ then What will be the ratio of amplitudes of two interfering waves?
A. $5:7$
B. $7:4$
C. $4:7$
D. $7:5$

Answer 1

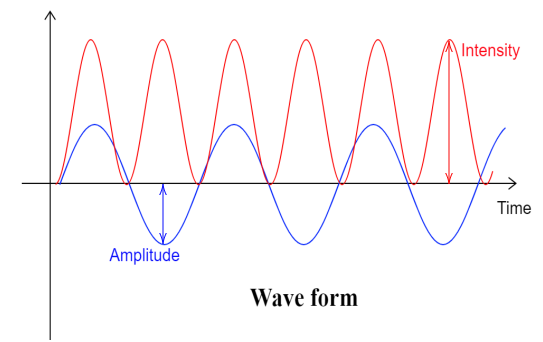
Hint: The wave interference pattern is formed when two waves intersect each other. While intersecting, the intensity will change according to the intensity of the two waves. Similarly, the amplitude also gets changed based on the amplitude of the two waves. Using the given ratio of intensity, the ratio of amplitude can be calculated.

Formula used:
In wave interference, the maximum intensity, ${I_{\max }} = {\left( {\sqrt {\dfrac{{{I_1}}}{{{I_2}}}} + 1} \right)^2}$
And the minimum intensity, ${I_{\min }} = {\left( {\sqrt {\dfrac{{{I_1}}}{{{I_2}}}} - 1} \right)^2}$
Also, the relation between intensity and amplitude,
$I \propto {A^2}$

Complete step by step answer:
Given, the ratio of maximum and minimum intensities in an interference pattern,
${I_{\max }}:{I_{\min }} = 36:1$

Thus, $\dfrac{{{I_{\max }}}}{{{I_{\min }}}} = \dfrac{{36}}{1}$
By substituting the values of ${I_{\max }}$ and ${I_{\min }}$ in above equation, we get
$\dfrac{{{{\left( {\sqrt {\dfrac{{{I_1}}}{{{I_2}}}} + 1} \right)}^2}}}{{{{\left( {\sqrt {\dfrac{{{I_1}}}{{{I_2}}}} - 1} \right)}^2}}} = \dfrac{{36}}{1}\;.....................................\left( 1 \right)$
Since, the relation between intensity and amplitude,
$I \propto {A^2}$
So, $A \propto \sqrt I $, used in equation (1).
$ \Rightarrow \dfrac{{{{\left( {\dfrac{{{A_1}}}{{{A_2}}} + 1} \right)}^2}}}{{{{\left( {\dfrac{{{A_1}}}{{{A_2}}} - 1} \right)}^2}}} = \dfrac{{36}}{1}\;$
Taking square root on both sides,
$ \Rightarrow \dfrac{{\left( {\dfrac{{{A_1}}}{{{A_2}}} + 1} \right)}}{{\left( {\dfrac{{{A_1}}}{{{A_2}}} - 1} \right)}} = \sqrt {36} \;$
By rearranging the terms, we get
$
   \Rightarrow \left( {\dfrac{{{A_1}}}{{{A_2}}} + 1} \right) = 6 \times \left( {\dfrac{{{A_1}}}{{{A_2}}} - 1} \right)\; \\
   \Rightarrow \left( {\dfrac{{{A_1} + {A_2}}}{{{A_2}}}} \right) = 6 \times \left( {\dfrac{{{A_1} - {A_2}}}{{{A_2}}}} \right)\; \\
 $
Canceling common tern in both sides,
$
   \Rightarrow \left( {{A_1} + {A_2}} \right) = 6\left( {{A_1} - {A_2}} \right) \\
   \Rightarrow {A_1} + {A_2} = 6{A_1} - 6{A_2} \\
 $
By performing arithmetic operations,
$
   \Rightarrow {A_2} + 6{A_2} = 6{A_1} - {A_1} \\
   \Rightarrow 7{A_2} = 5{A_1} \\
 $
Hence, the final ratio $\dfrac{{{A_1}}}{{{A_2}}} = \dfrac{7}{5}$
$\therefore {A_1}:{A_2} = 7:5$

$\therefore $ The ratio of amplitudes of two interfering waves is$7:5$. Hence, the option (D) is correct.

Note:
The intensity of the wave is directly proportional to the amplitude of the wave. When the amplitude gets increased, then the intensity gets increased. Intensity is proportional to the square of the amplitude. It means the negative side of the wave gets multiplied to the positive side to get intensity. Thus, the sign doesn’t matter in intensity.