Question

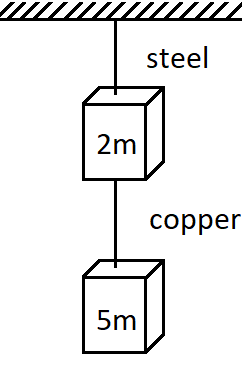
If the ratio of diameters, lengths and young’s modulus of steel and copper wires shown in the figure are $ p,q $ and $ s $ respectively, then the corresponding ratio of the increase in their lengths would be ________

Answer 1

Hint
By using the formula of the Young’s modulus of the wire we can find the formula for the increase in the length. Then we can take the ratio of the increase in length for both the wires. We can substitute the given values of the ratio of diameter, lengths and Young’s modulus. And the force on each wire will be the amount of weight on each of the wires.

Formula Used: In this solution we will be using the following formula,
 $ Y = \dfrac{{FL}}{{A\Delta L}} $
where $ Y $ is the young’s modulus
 $ F $ is the force
 $ L $ is the length
 $ A $ is the area and
 $ \Delta L $ is the change in the length.

Complete step by step answer
The young’s modulus of a wire is given by the formula,
 $ Y = \dfrac{{FL}}{{A\Delta L}} $
Here $ A $ is the area of the cross section of the wire. So we can write the area of cross section in the term of diameter of the wire as,
 $ A = \pi {\left( {\dfrac{D}{2}} \right)^2} $
Hence we get,
 $ A = \dfrac{{\pi {D^2}}}{4} $
So substituting this value in the formula we get,
 $ Y = \dfrac{{4FL}}{{\pi {D^2}\Delta L}} $
Now we can bring the $ \Delta L $ to the LHS and take the $ Y $ to the RHS. Therefore we get,
 $ \Delta L = \dfrac{{4FL}}{{\pi {D^2}Y}} $
Now let us consider the force, length, diameter and the young’s modulus of the steel wire be, $ {F_s} $, $ {L_s} $, $ {D_s} $ and $ {Y_s} $ respectively. Therefore, the change in length of the steel wire is,
 $ \Delta {L_s} = \dfrac{{4{F_s}{L_s}}}{{\pi {D_s}^2{Y_s}}} $
And for the copper wire let the force, length, diameter and the young’s modulus be, $ {F_c} $, $ {L_c} $, $ {D_c} $ and $ {Y_c} $ respectively. Therefore the change in length of the copper wire is,
 $ \Delta {L_c} = \dfrac{{4{F_c}{L_c}}}{{\pi {D_c}^2{Y_c}}} $
Now we can take the ratio of the change in lengths of the steel and copper wire as,
 $ \dfrac{{\Delta {L_s}}}{{\Delta {L_c}}} = \dfrac{{\dfrac{{4{F_s}{L_s}}}{{\pi {D_s}^2{Y_s}}}}}{{\dfrac{{4{F_c}{L_c}}}{{\pi {D_c}^2{Y_c}}}}} $
So the 4 and the $ \pi $ gets cancelled and we can simplify the form of this equation as,
 $ \dfrac{{\Delta {L_s}}}{{\Delta {L_c}}} = \dfrac{{{F_s}}}{{{F_c}}} \times \dfrac{{{L_s}}}{{{L_c}}} \times \dfrac{{{D_c}^2}}{{{D_s}^2}} \times \dfrac{{{Y_c}}}{{{Y_s}}} $
Now according to the diagram, the force on the steel wire is the sum of the weights of the two blocks. So we get, $ {F_s} = \left( {2m + 5m} \right)g = 7mg $
And the force on the copper wire is due to the weight of the second block only. Hence we get,
 $ {F_c} = 5mg $
In the question we are given the ratio of the lengths as, $ \dfrac{{{L_s}}}{{{L_c}}} = q $
The ratio of the diameters is given as, $ \dfrac{{{D_s}}}{{{D_c}}} = p $ and the ratio of the young’s modulus is given as, $ \dfrac{{{Y_s}}}{{{Y_c}}} = s $. Now substituting all the values in the equation we get,
 $ \dfrac{{\Delta {L_s}}}{{\Delta {L_c}}} = \dfrac{{7mg}}{{5mg}} \times q \times {\left( {\dfrac{1}{p}} \right)^2} \times \dfrac{1}{s} $
Hence on simplifying and cancelling the like terms we get,
 $ \dfrac{{\Delta {L_s}}}{{\Delta {L_c}}} = \dfrac{{7q}}{{5{p^2}s}} $
This is the corresponding ratio of the increase in lengths of the steel wire to the copper wire.

Note
The young’s modulus of a wire is the property of the material of a wire. This is the mechanical property that measures the tensile stiffness of a solid material. It can be given by the ratio of the tensile stress and the axial strain.