Question

If the position vector of a point A is \[\vec a + 2\vec b\] and \[\vec a\] divides \[\overrightarrow {AB} \] in the ratio 2:3, then the position vector of b is?
A.\[2\vec a - \vec b\]
B.\[\vec b - 2\vec a\]
C.\[\vec a - 3\vec b\]
D.\[\vec b\]

Answer 1

Hint: We are given a vector \[\overrightarrow {AB} \] such a way that the position vector of a point A is \[\vec a + 2\vec b\] and \[\vec a\] divides \[\overrightarrow {AB} \] in the ratio 2:3. We need to find the position vector of b. For that we will consider \[\vec x\] as position vector of b. then we will use the section formula.

Complete step-by-step answer:
Let’s get the problem with the help of a diagram.

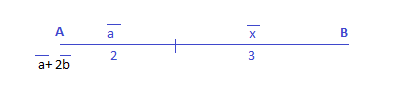
Now in the diagram above we can see that AB is divided in the ratio 2:3.
Let’s use the section formula then.
\[\vec a = \dfrac{{2\vec x + 3\left( {\vec a + 2\vec b} \right)}}{{2 + 3}}\]
\[ \Rightarrow \vec a = \dfrac{{2\vec x + 3\left( {\vec a + 2\vec b} \right)}}{5}\]
Cross multiplying with 5,
\[ \Rightarrow 5\vec a = 2\vec x + 3\vec a + 6\vec b\]
Taking position vector of b on one side separately,
\[ \Rightarrow 5\vec a - 3\vec a - 6\vec b = 2\vec x\]
On performing the necessary mathematical operations,
\[ \Rightarrow 2\vec x = 2\vec a - 6\vec b\]
Dividing both sides by 2,
\[ \Rightarrow \vec x = \vec a - 3\vec b\]
And this is our answer for the position vector of b equals \[\vec x = \vec a - 3\vec b\]
So the correct option is C.

Note: Section formula is used when a vector divides a segment either internally or externally. Here we have used internal division as shown in the diagram. If the point is somewhere on the segment then we call it internal division and if it is dividing the segment but not on segment then we call it external division.