Question

If the points A(1,2), B(2,3), C(a,2) and D(4,3) form a parallelogram, find the value of a and the height of the parallelogram taking AB as base.
$
  (a){\text{ a = 1,h = 2}} \\
  (b){\text{ a = 1,h = 1}} \\
  (c){\text{ a = 3,h = 1}} \\
  (d){\text{ a = 2,h = 3}} \\
 $

Answer 1

Hint – In this question use the distance formula to calculate the length of base AB. Use the concept that opposite sides of a parallelogram are equal, thus the value of a can be calculated. To find height consider the fact that a diagonal of a parallelogram divides it into two equal triangles of equal areas.
Complete step-by-step answer:

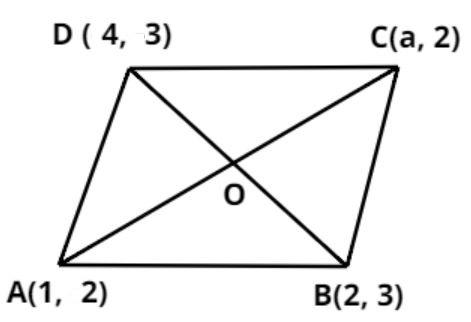
Let us consider the parallelogram ABCD as shown above.
Let A = (x₁, y₁) = (1, 2), B = (x₂, y₂) = (2, 3), C = (x₃, y₃) = (a, 2), D = (x₄, y₄) = (4, 3).
As we know that in parallelogram the length of opposite sides are equal.
Therefore length of AB = BC
Now as we know that the distance (d) between two points (x₁, y₁) , (x₂, y₂) is calculated as,
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
Therefore AB = $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {3 - 2} \right)}^2}} = \sqrt 2 $
Now distance CD = $\sqrt {{{\left( {{x_4} - {x_3}} \right)}^2} + {{\left( {{y_4} - {y_3}} \right)}^2}} = \sqrt {{{\left( {4 - a} \right)}^2} + {{\left( {3 - 2} \right)}^2}} = \sqrt {{{\left( {4 - a} \right)}^2} + 1} $
$ \Rightarrow \sqrt 2 = \sqrt {{{\left( {4 - a} \right)}^2} + 1} $
Now squaring on both sides we have,
$ \Rightarrow 2 = {\left( {4 - a} \right)^2} + 1$
$ \Rightarrow {\left( {4 - a} \right)^2} = 1$
$ \Rightarrow 4 - a = \sqrt 1 = 1$
$ \Rightarrow a = 4 - 1 = 3$
Now as we know that the area of the parallelogram (ABCD) = $2 \times $area of triangle ABD.
So first calculate area of triangle ABD
So area of triangle ABD = $\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|$
Let A = (x₁, y₁) = (1, 2)
B = (x₂, y₂) = (2, 3)
D = (x₃, y₃) = (4, 3)
Therefore area (A) of triangle ABD = $\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  1&2&1 \\
  2&3&1 \\
  4&3&1
\end{array}} \right|$
Now expand the determinant we have,
A = $\dfrac{1}{2}\left[ {1\left| {\begin{array}{*{20}{c}}
  3&1 \\
  3&1
\end{array}} \right| - 2\left| {\begin{array}{*{20}{c}}
  2&1 \\
  4&1
\end{array}} \right| + 1\left| {\begin{array}{*{20}{c}}
  2&3 \\
  4&3
\end{array}} \right|} \right]$
Now simplify it we have,
A = $\dfrac{1}{2}\left[ {1\left( {3 - 3} \right) - 2\left( {2 - 4} \right) + 1\left( {6 - 12} \right)} \right]$
A = $\dfrac{1}{2}\left[ {0 + 4 - 6} \right] = \dfrac{{ - 2}}{2} = - 1$ sq. units.
Now as we know area cannot be negative so we calculate the absolute value,
$ \Rightarrow A = 1$ Sq. units.
So the area of parallelogram = $2 \times 1 = 2$ sq. units.
Now as we know that the area of the triangle is half multiplied by base (b) and height (h).
So area of parallelogram = $2 \times \dfrac{1}{2} \times h \times b$
$ \Rightarrow h = \dfrac{2}{b}$ unit.
Now it is given that AB is the base.
So the distance of AB is calculated as
$ \Rightarrow AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
A = (x₁, y₁) = (1, 2)
B = (x₂, y₂) = (2, 3)
So the distance AB is
$ \Rightarrow AB = b = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {3 - 2} \right)}^2}} = \sqrt {1 + 1} = \sqrt 2 $ unit.
So the height of the parallelogram is
$ \Rightarrow h = \dfrac{2}{{\sqrt 2 }} = \sqrt 2 $ unit.
So this is the required height of the parallelogram.

Note – Here we have used the direct determinant formula to compute the area of triangles when coordinates of its all three sides are given that is $\dfrac{1}{2}\left| {\begin{array}{*{20}{c}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|$, it is advised to remember this short trick formula. Some properties of parallelogram are also helpful in solving problems of this kind like the opposite angles are congruent of a parallelogram, consecutive angles are supplementary and the diagonals of a parallelogram bisects each other.