Question

If the points \[(-1,-1,2),(2,m,5)\,and\,(3,11,6)\] are collinear, then find the value of m.
(A). 6
(B). 8
(C). 10
(D). 12

Answer 1

Hint: Assume three points P, Q, and R whose coordinates are \[(-1,-1,2),(2,m,5)\,and\,(3,11,6)\] respectively. Express the coordinates of the points P, Q, and R in the vector form as \[\overrightarrow{P}=-1\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,+2\overset{\hat{\ }}{\mathop{k}}\,\] , \[\overrightarrow{Q}=2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,\] , and \[\overrightarrow{R}=3\overset{\hat{\ }}{\mathop{i}}\,+11\overset{\hat{\ }}{\mathop{j}}\,+6\overset{\hat{\ }}{\mathop{k}}\,\] . If the points P, Q, and R is collinear then,\[\overrightarrow{PQ}=\lambda \overrightarrow{QR}\] where \[\overrightarrow{PQ}=\overrightarrow{P}-\overrightarrow{Q}\] and \[\overrightarrow{QR}=\overrightarrow{Q}-\overrightarrow{R}\] . Now compare LHS and RHS and solve it further.

Complete step-by-step solution -
Assume three points P, Q, and R whose coordinates are \[(-1,-1,2),(2,m,5)\,and\,(3,11,6)\] respectively.
If three points are collinear then all the three points lie on the same line.

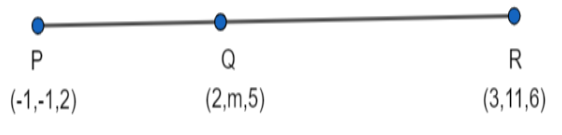
Express the coordinates of the points P, Q, and R in the vector form.
Converting the coordinates of the points P, Q, and R in the vector form, we get
\[\overrightarrow{P}=-1\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,+2\overset{\hat{\ }}{\mathop{k}}\,\] ……………….(1)
\[\overrightarrow{Q}=2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,\] ……………….(2)
\[\overrightarrow{R}=3\overset{\hat{\ }}{\mathop{i}}\,+11\overset{\hat{\ }}{\mathop{j}}\,+6\overset{\hat{\ }}{\mathop{k}}\,\] ……………….(3)
If the points P, Q, and R is collinear then,
\[\overrightarrow{PQ}=\lambda \overrightarrow{QR}\] …………….(4)
Now, the value of the \[\overrightarrow{PQ}\] is,
\[\overrightarrow{PQ}=\overrightarrow{P}-\overrightarrow{Q}\] ……………..(5)
Putting the value of \[\overrightarrow{P}\] and \[\overrightarrow{Q}\] from equation (1) and equation (2) in equation (5), we get
\[\overrightarrow{PQ}=(-1\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,+2\overset{\hat{\ }}{\mathop{k}}\,)-(2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,)\]
\[\Rightarrow \overrightarrow{PQ}=-3\overset{\hat{\ }}{\mathop{i}}\,-(m+1)\overset{\hat{\ }}{\mathop{j}}\,-3\overset{\hat{\ }}{\mathop{k}}\,\] ……………………(6)
Now, the value of the \[\overrightarrow{QR}\] is,
\[\overrightarrow{QR}=\overrightarrow{Q}-\overrightarrow{R}\] ……………..(7)
Putting the value of \[\overrightarrow{Q}\] and \[\overrightarrow{R}\] from equation (2) and equation (3) in equation (7), we get
\[\overrightarrow{QR}=2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,-3\overset{\hat{\ }}{\mathop{i}}\,-11\overset{\hat{\ }}{\mathop{j}}\,-6\overset{\hat{\ }}{\mathop{k}}\,\]
\[\Rightarrow \overrightarrow{QR}=-1\overset{\hat{\ }}{\mathop{i}}\,+(m-11)\overset{\hat{\ }}{\mathop{j}}\,-1\overset{\hat{\ }}{\mathop{k}}\,\] ………………………(8)
From equation (4), we have \[\overrightarrow{PQ}=\lambda \overrightarrow{QR}\] .
Now, putting the value of \[\overrightarrow{PQ}\] and \[\overrightarrow{QR}\] from equation (6) and equation (8) in equation (4), we get
\[\overrightarrow{PQ}=\lambda \overrightarrow{QR}\]
\[\Rightarrow -3\overset{\hat{\ }}{\mathop{i}}\,-(m+1)\overset{\hat{\ }}{\mathop{j}}\,-3\overset{\hat{\ }}{\mathop{k}}\,=\lambda \{-1\overset{\hat{\ }}{\mathop{i}}\,+(m-11)\overset{\hat{\ }}{\mathop{j}}\,-1\overset{\hat{\ }}{\mathop{k}}\,\}\]
On comparing LHS and RHS of the above equation, we get
\[-3=-\lambda \] ……………………..(9)
\[-(m+1)=\lambda (m-11)\] ………………….(10)
Solving equation (1), we get
\[-3=-\lambda \]
\[\Rightarrow 3=\lambda \] …………………(11)
Now, putting the value of \[\lambda \] in equation (10), we get
\[-(m+1)=\lambda (m-11)\]
\[\begin{align}
  & -(m+1)=3(m-11) \\
 & \Rightarrow -m-1=3m-33 \\
 & \Rightarrow 33-1=3m+m \\
 & \Rightarrow 32=4m \\
 & \Rightarrow 8=m \\
\end{align}\]
So, the value of m is 8.
Hence, the correct option is (B).

Note: We can also solve this question using another method.
If the points \[\overrightarrow{P}=-1\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,+2\overset{\hat{\ }}{\mathop{k}}\,\] , \[\overrightarrow{Q}=2\overset{\hat{\ }}{\mathop{i}}\,+m\overset{\hat{\ }}{\mathop{j}}\,+5\overset{\hat{\ }}{\mathop{k}}\,\] and \[\overrightarrow{R}=3\overset{\hat{\ }}{\mathop{i}}\,+11\overset{\hat{\ }}{\mathop{j}}\,+6\overset{\hat{\ }}{\mathop{k}}\,\] are collinear then \[\overrightarrow{PQ}=-3\overset{\hat{\ }}{\mathop{i}}\,-(m+1)\overset{\hat{\ }}{\mathop{j}}\,-3\overset{\hat{\ }}{\mathop{k}}\,\] must be parallel to \[\overrightarrow{QR}=-1\overset{\hat{\ }}{\mathop{i}}\,+(m-11)\overset{\hat{\ }}{\mathop{j}}\,-1\overset{\hat{\ }}{\mathop{k}}\,\] .
Hence, the ratios of corresponding direction ratios of parallel \[\overrightarrow{PQ}=-3\overset{\hat{\ }}{\mathop{i}}\,-(m+1)\overset{\hat{\ }}{\mathop{j}}\,-3\overset{\hat{\ }}{\mathop{k}}\,\] and \[\overrightarrow{QR}=-1\overset{\hat{\ }}{\mathop{i}}\,+(m-11)\overset{\hat{\ }}{\mathop{j}}\,-1\overset{\hat{\ }}{\mathop{k}}\,\] must be equal.
So, \[\dfrac{-3}{-1}=\dfrac{-(m+1)}{(m-11)}=\dfrac{-3}{-1}\] .
Now,
\[\begin{align}
  & \dfrac{-3}{-1}=\dfrac{-(m+1)}{(m-11)} \\
 & \Rightarrow -3\left( m-11 \right)=\left( m+1 \right) \\
 & \Rightarrow -3m+33=m+1 \\
 & \Rightarrow 33-1=3m+m \\
 & \Rightarrow 32=4m \\
 & \Rightarrow 8=m \\
\end{align}\]
So, the value of m is 8.
Hence, the correct option is (B).