Question

If the point $\left( 3,-2 \right)$ is transformed to $\left( -2,1 \right)$ when the origin is shifted to $P$, then $P=$? \[\]
A.$\left( 3,2 \right)$ \[\]
B.$\left( 5,-3 \right)$ \[\]
C. $\left( 2,-3 \right)$ \[\]
D.$\left( -1,2 \right)$ \[\]

Answer 1

Hint: We recall the definition of origin, shifting of origin and translation of axes . We use the knowledge that if the origin is shifted from $O\left( 0,0 \right)$ to ${{O}^{'}}\left( h,k \right)$ then any point $A\left( x,y \right)$in the original coordinate system will have coordinates ${{A}^{'}}\left( x-h,y-k \right)$ in the new coordinate system \[\]

Complete step-by-step answer:
We know that in the Cartesian coordinate system we take two perpendicular lines as reference axes which we call as coordinate axes. The horizontal axis is denoted as $X-$axis and the vertical line is called $Y-$axis. The point of intersection of $X-$axis and $Y-$axis is called origin denoted conventionally as O. The coordinate of any point A is denoted by an ordered pair $A\left( x,y \right)$ where $x$is the perpendicular distance of A from $Y-$axis called abscissa and $y$ is the perpendicular distance of A from $Y-$axis called ordinate. Since origin lies on both $X$ and $Y$-axis its coordinate is $O\left( 0,0 \right)$. \[\]
If the origin is shifted to a point ${{O}^{'}}\left( h,k \right)$ then axes will also be shifted to accommodate the new origin. The $X-$axis shift by distance $\left| h \right|$ and will become the new coordinate axis, say ${{X}^{'}}$. The $Y-$axis will shift by distance $\left| k \right|$ and will become the new coordinate axis say ${{Y}^{'}}$. \[\]

 

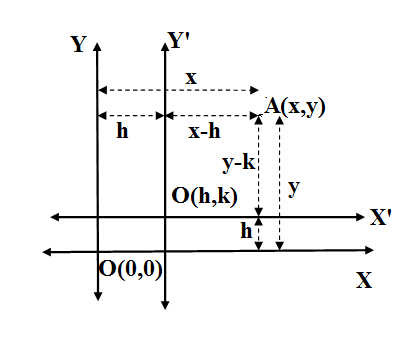
If $A\left( x,y \right)$ is a point in the original $XY$ coordinate system then its new coordinate in ${{X}^{'}}{{Y}^{'}}$ coordinate system will be ${{A}^{'}}\left( x-h,y-k \right)$. \[\]
We are given the question that the point $\left( 3,-2 \right)$ is transformed to $\left( -2,1 \right)$. The origin o shifted to P. Let us denote the new origin as $P\left( h,k \right)$. If we assign the original point as $A\left( 3,2 \right)$, the new point will be ${{A}^{'}}\left( -2,1 \right)$. So we have $\left( x,y \right)=\left( 3,2 \right)$ and$\left( x-h,y-k \right)=\left( -2,1 \right)$. Then we have;
\[\begin{align}
  & s\left( x-h,y-k \right)=\left( -2,1 \right) \\
 & \Rightarrow \left( 3-h,-2-k \right)=\left( -2,1 \right)\left( \because \left( x,y \right)=\left( 3,-2 \right) \right) \\
 & \Rightarrow 3-h=-2,-2-k=1 \\
 & \Rightarrow h=3+2=5,k=-2-1=-3 \\
 & \Rightarrow \left( h,k \right)=\left( 5,-3 \right) \\
\end{align}\]
So the coordinate of P is $P\left( 5,-3 \right)$
So, the correct answer is “Option B”.

Note: We know that two ordered pairs are equal when the elements are equal in order which means$\left( a,b \right)=\left( c,d \right)\Rightarrow a=b\text{ and }c=d$. If $A\left( x,y \right)$ is the original coordinate and $A\left( {{x}^{'}},{{y}^{'}} \right)$ is the new coordinate then they are related as $x={{x}^{'}}+h,y={{y}^{'}}+k$. We must be careful of the difference between translation of axes and rotation of axes where the relation between new and old coordinates is $x={{x}^{'}}\cos \theta -{{y}^{'}}\sin \theta ,y={{x}^{'}}\sin \theta +{{y}^{'}}\cos \theta $ with angle of rotation $\theta $.