Question

If the perimeter of the equilateral triangle is 180 cm, what will be its area?

Answer 1

Hint: Assume any variable be the side of an equilateral triangle then use the concept that perimeter of any shape is the sum of all the sides later on use the direct formula of the area of the equilateral triangle so use these concepts to reach the solution of the question.

Complete step-by-step answer:

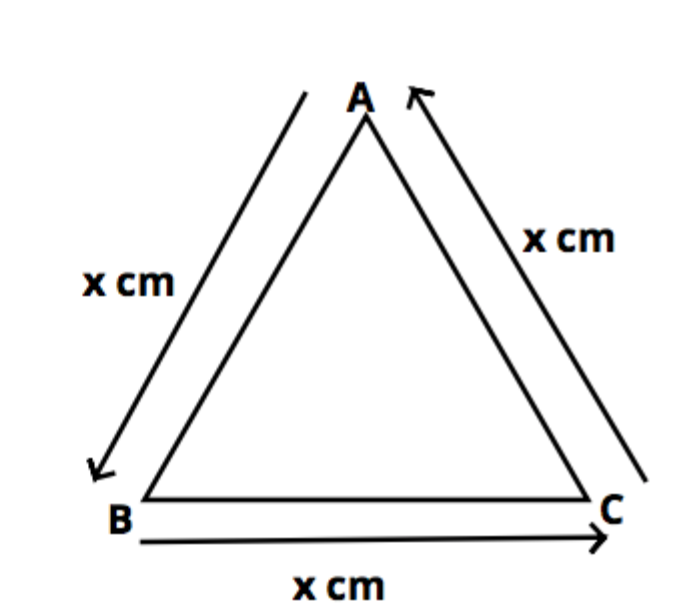
Let the side of the equilateral triangle be x cm as shown in figure.

As we know that all sides of an equilateral triangle are equal, thus AB=BC=CA = x cm……………. (1)

Perimeter of $\vartriangle ABC$= 180cm.

Now perimeter is the sum of all the sides,

Thus perimeter $\vartriangle ABC$ will be AB+BC+CA = 180 ……………….. (2)

Substituting values from equation (1) into equation (2) we get

x + x + x = 180

$

   \Rightarrow 3x = 180 \\

   \Rightarrow x = 60 \\

$

So the side of an equilateral triangle is 60cm.

Area of the equilateral triangle is given as ${\text{Area = }}\dfrac{{\sqrt 3 }}{4}{x^2}$ where x is the side of the equilateral triangle.

So substituting the value of x in formula of area we get,

$

  {\text{Area = }}\dfrac{{\sqrt 3 }}{4} \times {(60)^2} \\

   \Rightarrow 900\sqrt 3 \\

   \Rightarrow 1558.84{\text{ c}}{{\text{m}}^2} \\

$

Hence the area of the triangle is 1558.84$c{m^2}$.

Note: Whenever we face such types of questions the key concept is always recall the formula of equilateral triangle so first find out the side of equilateral triangle as perimeter of equilateral triangle is given so calculate its side as above than substitute this side value in the formula of area as above and simplify we will get the required answer.