Question

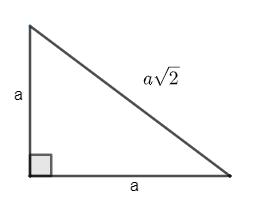
If the perimeter of a right-angles isosceles triangle is $\sqrt{2}+1$ , then what is the length of the hypotenuse?

(a)$\dfrac{1}{\sqrt{2}}cm$
(b)$\sqrt{2}cm$
(c)$1cm$
(d)$2cm$

Answer 1

Hint: Apply the given condition to get all sides in terms of one variable itself. Now by using the condition of perimeter find the value of the variable by using this variable find the value of hypotenuse. This length of hypotenuse is the required result.

Complete step-by-step answer:
Given condition in the question is written as, an isosceles right angled triangle has perimeter $\sqrt{2}+1$
Isosceles triangle: When two side lengths of a triangle are equal then it is said to be an isosceles triangle.
Right angled triangle: A triangle whose one of the angles is ${{90}^{\circ }}$ is called a right angled triangle. It always follow Pythagora's theorem.
Given triangle is isosceles right angle triangle. Hypotenuse is always greater than other sides. So, the only possibility of isosceles is base being equal to height. Let us assume the length of base is given by ‘a’ cm. BY previous explanation length of height is also a cm. If the triangle is ABC right angled at B.
By our assumption, we can write it as,
AB = BC = a

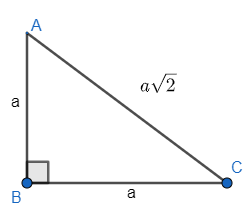
The sum of the square of base and height is equal to the square of hypotenuse. This is called Pythagoras theorem for right angles triangle.
By applying Pythagoras theorem, we get the equation as,
$A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$
By substituting the values, we can write them as follows,
$A{{C}^{2}}={{a}^{2}}+{{a}^{2}}$
By simplifying, we can write the equation in form of,
$A{{C}^{2}}=2{{a}^{2}}$
By applying square root on both sides of equation we get,
$AC=\sqrt{2{{a}^{2}}}=\sqrt{2a}................(1)$
The perimeter of this triangle is sum of all sides,
AB + BC + CA = perimeter
By substituting all values we get it as,
$a+a+\sqrt{2}=\sqrt{2}+1\Rightarrow \left( \sqrt{2}+2 \right)a=\sqrt{2}+1$
By taking $\sqrt{2a}$ common we can write it as,
$\sqrt{2a}\left( \sqrt{2}+1 \right)=\sqrt{2}+1$
By cancelling common terms, we get value of ‘a’ as
$a=\dfrac{1}{\sqrt{2}}$
By substituting in equation (1) we get it in form of,
$AC=\sqrt{2}\left( \dfrac{1}{\sqrt{2}} \right)=1cm$
So, hypotenuse is 1cm for a given triangle. Therefore option (c) is correct.

Note: Be careful with definitions as they are base for our solution while making base, height are equal sided the point of hypotenuse greater is very important idea. Be careful while substituting in the perimeter. In a hurry students write $\sqrt{2}+1$ instead of $\sqrt{2}+2$ , and get the wrong value for ‘a’. Be careful at this step.