Question

If the pair of equations has no solution, then the pair of equation is:
(a) Consistent
(b) Inconsistent
(c) Coincident
(d) None of these

Answer 1

Hint: First of all, we consider all the types of equations which have only one solution, no solution or many solutions and then on the basis of that we will solve the problem by eliminating the option method and find the final answer.

Complete step by step solution:
In the question it is give that pair of equation has no solution, so first of all we will see the type of pair of equations that is:
In type I: If the pair of equations has a unique solution then two lines intersect each other at only one point so we can say that the pair of equations is consistent. Example is shown below.

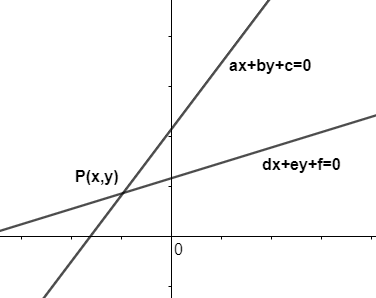
In type II: If the pair of equations have many solutions then the lines intersect each other in many points, so here we can say that pair of equations is consistent. For example, it is shown in the diagram.

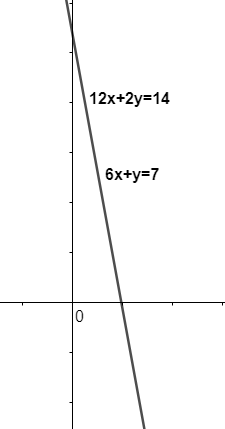
In type III: If a pair of equations are parallel then the lines do not intersect each other at any point till infinite, so, we can say that the pair of equations is inconsistent.

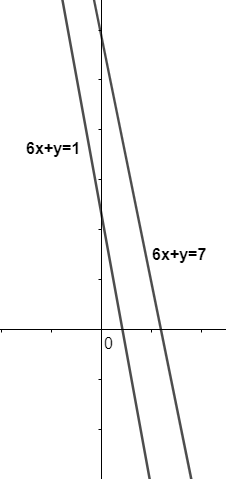
Now, based on the three types of solutions we will compare our options with each type and find the answer.
So, in question it is given that a pair of equations has no solution, so, looking on all the three types we can say that the third type satisfies the condition. So, according to that we can say that the pair of equations is inconsistent.
Hence, option (b) is the correct answer.

Note: Taking an example of a consistent, inconsistent and coincident pair of equations. Consider two equation i.e. ${{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0,{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0,$
if $\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}$ then, the linear equations pair is consistent.
Now, if $\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}}$ then the lines are coincident and the pair of equation is dependent and consistent.
And if $\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}\ne \dfrac{{{c}_{1}}}{{{c}_{2}}}$ then pair of equation are called inconsistent because those linear equation are parallel to each other so, no solution exists in such case.
So, remember these three conditions while solving the problem.