Question

If the lines $l$, m and n are such that $l\parallel m$ and \[m\parallel n\], then:
A.$l\parallel n$
B.$l \bot n$
C.$l$and n are intersecting
D.None of these

Answer 1

Hint: Let us first of all discuss about parallel lines, parallel lines are the lines which do not intersect at any point up to infinity i.e. they never meet nor at infinity.
In this question three lines are given $l$, m & n and it is given that $l\parallel m$and \[m\parallel n\].
Now consider both the conditions together then analyse which option is true and why? This is shown with the help of a diagram as below:

Here $l\parallel m$and \[m\parallel n\]. Relate both the diagrams and give the conclusion.

Complete step-by-step answer:
We will discuss every option one by one and the reason for the conclusion.
Start with option A. In option A they say that $l\parallel n$.
Now, check whether it is true or not? See both the diagram and try to make the conclusion.
It explained with the help of diagrams shown below:

As you see above figure three lines are there $l$, m & n and $l\parallel m$& \[m\parallel n\]. Therefore, from the above figure it is clear that $l\parallel n$. You can see they can never meet i.e. l and n so they are parallel.

Check option B i.e. $l \bot n$. As, we know $l\parallel m$& \[m\parallel n\]. If l is parallel to n then relate it with given condition as shown

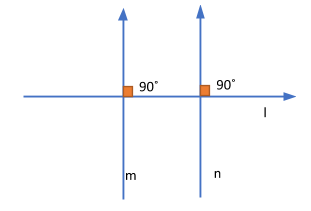
Here, you can see if we consider this option i.e. $l \bot n$, then $l \bot m$ which is not possible hence, this option is wrong.
As they both are parallel so they never intersect each other. Hence, this option is also wrong.
So, option A is the correct answer.

Note: If two lines are parallel and there is one transversal line cut both the lines then their corresponding angle and alternate angles are equal.
Corresponding angles: The angles which are on the same side of the transversal line are known as corresponding angles.
Alternate angles: - The angles which are inside the both lines and are at opposite sides are known as alternate angles.