Question

If the line $x-y-1=0,4x+3y=k$ and $2x=3y+1=0$ are concurrent, then $k$ is.
A. 1
B. -1
C. 25
D. 5

Answer 1

Hint: If three lines ${{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0,{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0,$ and ${{a}_{3}}x+{{b}_{3}}y+{{c}_{3}}=0$ are concurrent then the determinant$\left( \begin{matrix}
   {{a}_{1}} & {{b}_{1}} & {{c}_{1}} \\
   {{a}_{2}} & {{b}_{2}} & {{c}_{2}} \\
   {{a}_{3}} & {{b}_{3}} & {{c}_{3}} \\
\end{matrix} \right)$$\left( \begin{matrix}
   {{a}_{1}} & {{b}_{1}} & {{c}_{1}} \\
   {{a}_{2}} & {{b}_{2}} & {{c}_{2}} \\
   {{a}_{3}} & {{b}_{3}} & {{c}_{3}} \\
\end{matrix} \right)$ will equal to zero.
Solve the determinant and get the value of ’k’.

Complete step-by-step answer:
As, we know that concurrent means have only one intersection point. So, if three lines are concurrent, then they should meet at only one point.
Now, condition for concurrency of three lines are
${{a}_{1}}x+{{b}_{1}}x+{{c}_{1}}=0,{{a}_{2}}x+{{b}_{2}}x+{{c}_{2}}=0$ and${{a}_{3}}x+{{b}_{3}}x+{{c}_{3}}=0$ can be given as
$\left( \begin{matrix}
   {{a}_{1}} & {{b}_{1}} & {{c}_{1}} \\
   {{a}_{2}} & {{b}_{2}} & {{c}_{2}} \\
   {{a}_{3}} & {{b}_{3}} & {{c}_{3}} \\
\end{matrix} \right)=0$ ……………………………………………………………….(i)
So, now we have lines given as
$x-y-1=0$ and
$4x+3y=k$
or
$4x+3y-k=0$
and $2x-3y+1=0$
Now, we can compare the above lines with the mentioned lines in starting of solution and get the values of ${{a}_{1}},{{b}_{1}},{{c}_{1}}$, ${{a}_{2}},{{b}_{2}},{{c}_{2}}$ and ${{a}_{3}},{{b}_{3}},{{c}_{3}}$.

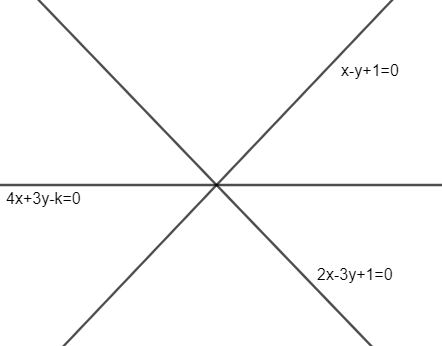
Hence, we can form a determinant as given in equation as
$\left( \begin{matrix}
   1 & -1 & -1 \\
   4 & 3 & -k \\
   2 & -3 &1 \\
\end{matrix} \right)=0$
Now, let us expand the determinant through Row 1. And hence, we get
$1\left( 3\times 1-\left( -3 \right)\left( -k \right) \right)+1\left( 4\times 1-\left( -k \right)\left( 2 \right) \right)-1\left( 4\times \left( -3 \right)-2\times 3 \right)$
On simplifying the above equation, we get
$\left( 3-3k \right)+\left( 4+2k \right)-1\left( -12-6 \right)$
$3-3k+4+2k+18=0$
And hence, we get
$-k+25=0$
$k=25$
Hence, if the given lines in the problem is constant, then value k should be 25.
Therefore option (C) is correct.

Note: Another approach for getting value of k that we can solve first and third equation to get value of ‘$ax+by+{{c}_{2}}=0$’ and ‘$y$’ and now put it with line second to get ‘k’ as all three lines have same intersecting point by definition of concurrency of lines.
One can go wrong if put ${{c}_{2}}=k$ in the determinant as line $4x+3y=k$ is not in the standard form i.e. $ax+by+c=0$. So, first write it in the standard form then substitute the values in the determinant. Hence, ${{c}_{2}}$ should be ‘-k ’ according to the standards.
Determinant used in the solution can be proved by using the formula of the area of the triangle.
The area formed with the concurrent lines should be zero. Hence, one can get the same determinant as given in the solution.