
If the line $ax + by + c = 0$ is such that \[{\text{a}} = 0\]
And \[{\text{b}}, {\text{c}} \ne 0, \]then the line is perpendicular to?
A.$x - axis$
B.$y - axis$
C.$x = y = 1$
D.$x = y$
Answer
572.4k+ views
Hint:- If a line is perpendicular to another line or axis,
It means the angle between these two lines or one line and axis is ${90^ \circ} $
Complete step by step by solution
Here we have given equation of line is
$ax + by + c = 0............... (1)$
and also given that that \[{\text{a}} = 0\]
And \[{\text{b}},{\text{c}} \ne 0,\]
Now to find position of the line put \[{\text{a}} = 0\]in equation 1
$0.x + by + c = 0$
$by + c = 0$
$y = - \dfrac{c}{b}$
i.e.
Value of y is $\dfrac{{ - c}}{b}$ for this equation. It will remain the same for all values of $x$.
Now we will show this value on a graph as shown below.
.
y
X’ x
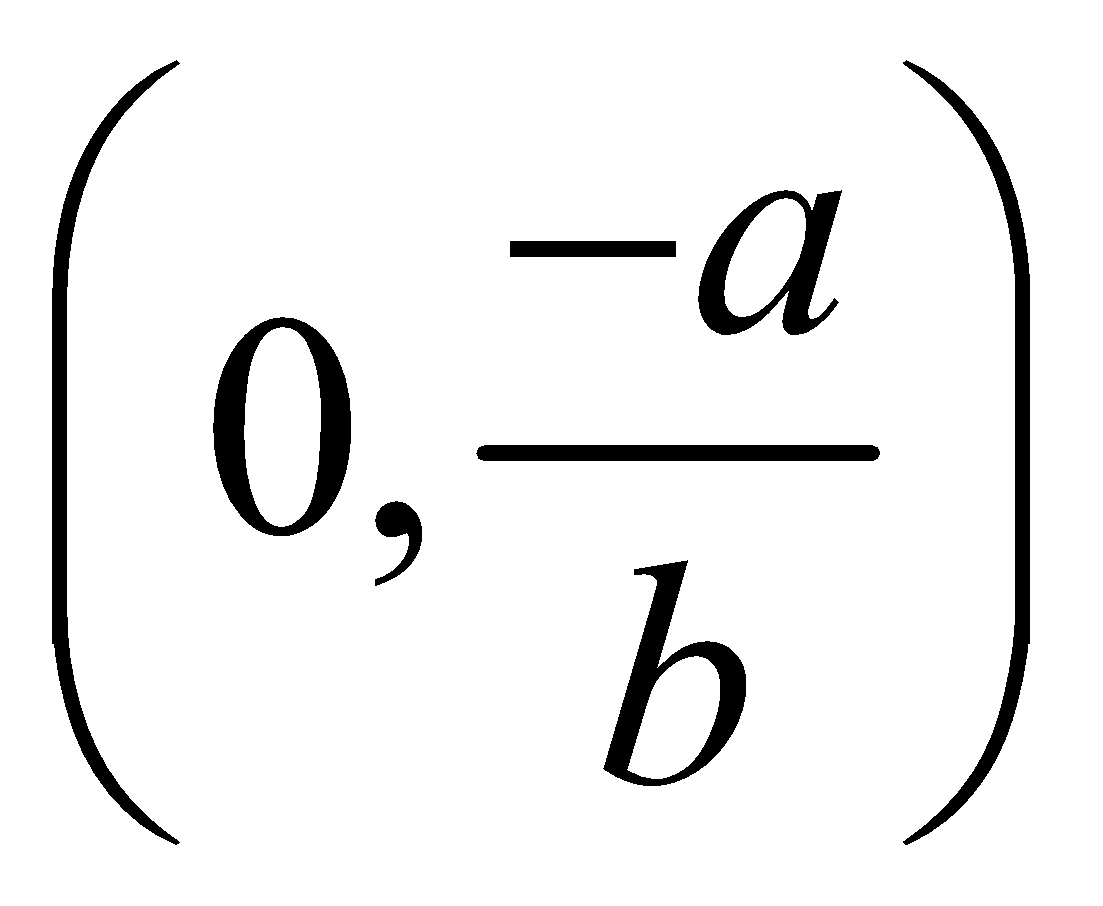
y’
y
X’ x
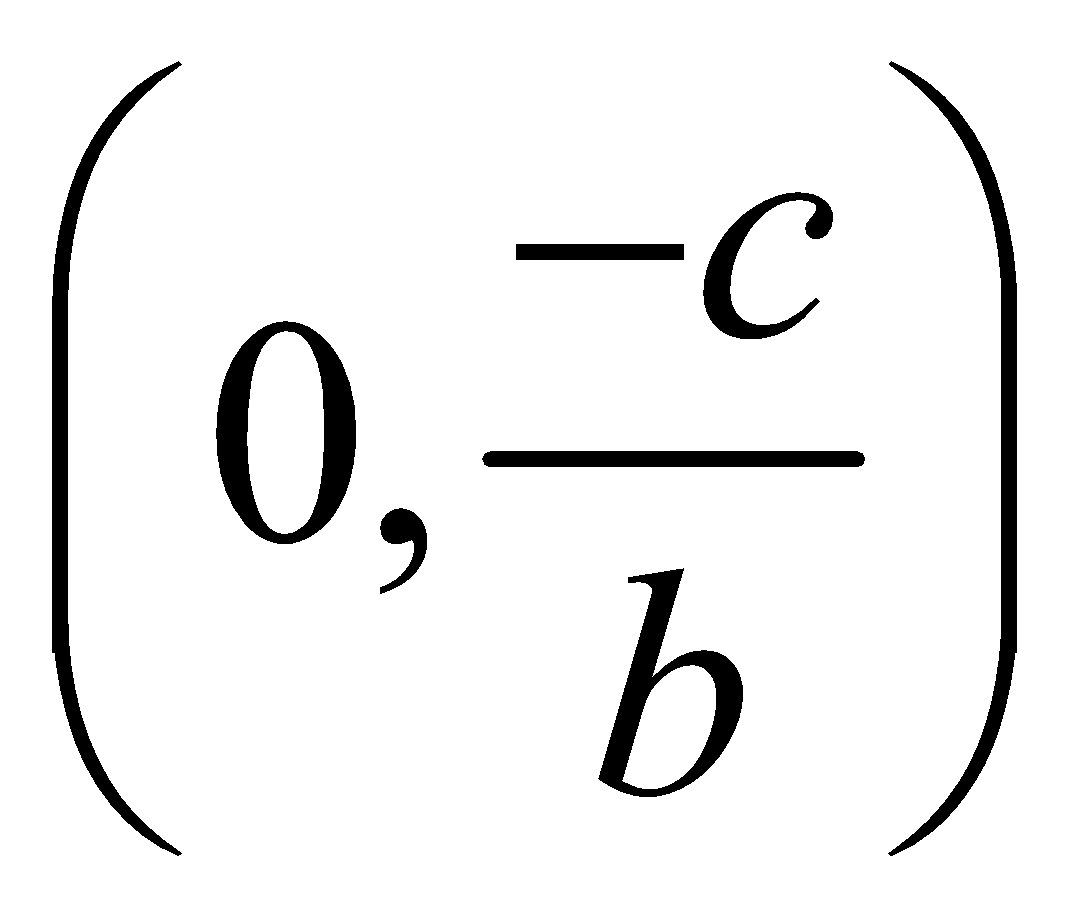
Here we can see that the line is perpendicular to y-axis and parallel to x-axis,
So (B) will be the right option.
Note –Remember if a line is perpendicular to y-axis then it will be parallel to x-axis
And value of y is fixing at ever for all values of x and if a line is perpendicular to x-axis
Then it will be parallel to the y-axis and the value of x is fixed for all values of y.
It means the angle between these two lines or one line and axis is ${90^ \circ} $
Complete step by step by solution
Here we have given equation of line is
$ax + by + c = 0............... (1)$
and also given that that \[{\text{a}} = 0\]
And \[{\text{b}},{\text{c}} \ne 0,\]
Now to find position of the line put \[{\text{a}} = 0\]in equation 1
$0.x + by + c = 0$
$by + c = 0$
$y = - \dfrac{c}{b}$
i.e.
Value of y is $\dfrac{{ - c}}{b}$ for this equation. It will remain the same for all values of $x$.
Now we will show this value on a graph as shown below.
.
y
X’ x
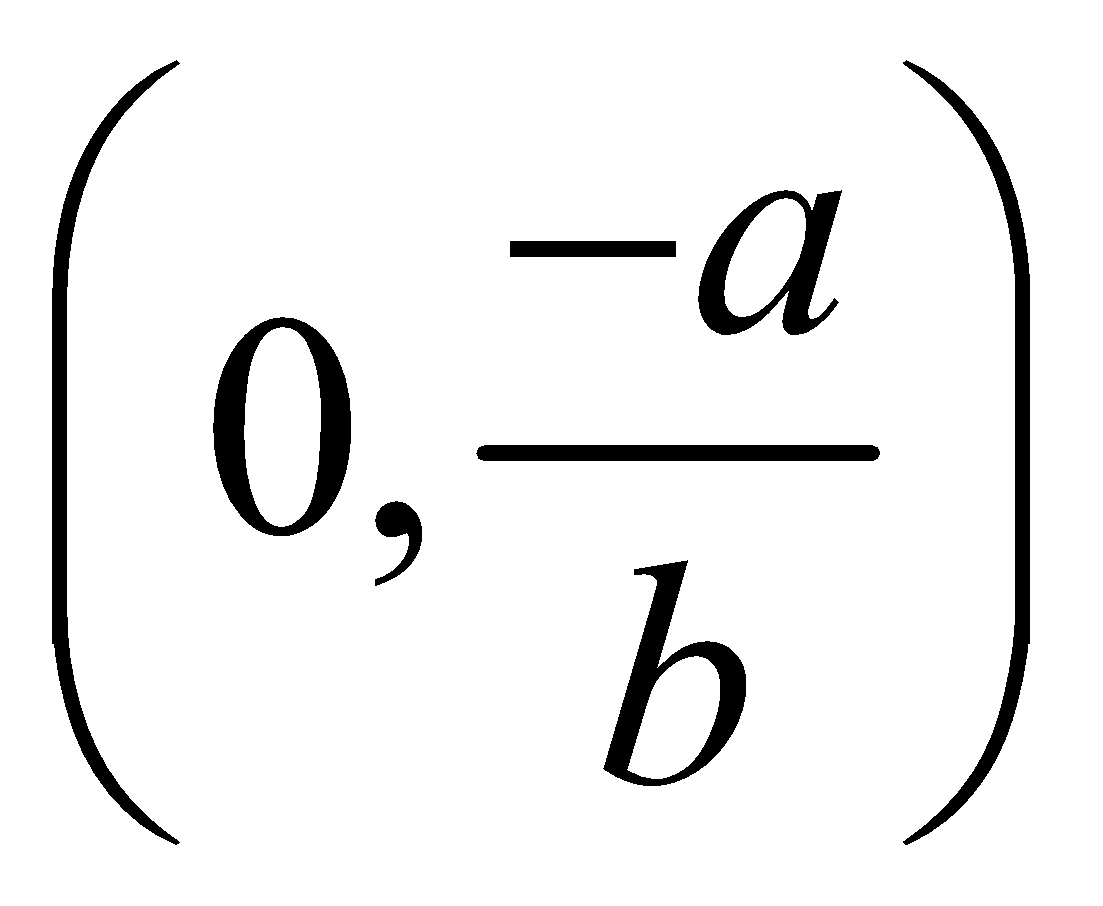
y’
y
X’ x
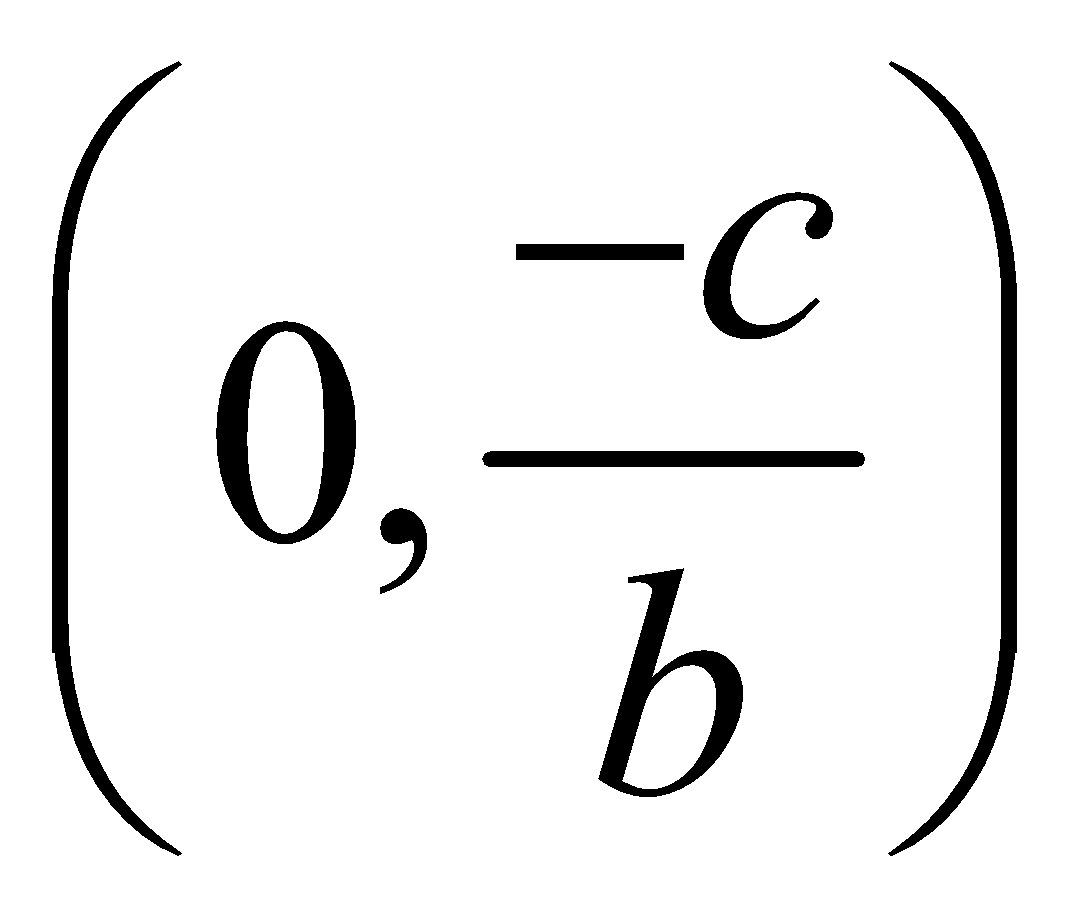
Here we can see that the line is perpendicular to y-axis and parallel to x-axis,
So (B) will be the right option.
Note –Remember if a line is perpendicular to y-axis then it will be parallel to x-axis
And value of y is fixing at ever for all values of x and if a line is perpendicular to x-axis
Then it will be parallel to the y-axis and the value of x is fixed for all values of y.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




