Question

If the length of the perpendicular from the point \[\left( \beta ,0,\beta \right)\left( \beta \ne 0 \right)\]to the line, \[\dfrac{x}{1}=\dfrac{y-1}{0}=\dfrac{z+1}{-1}\]is \[\sqrt{\dfrac{3}{2}}\], then \[\beta \] is equal to:
A. -1
B. 2
C. -2
D. 1

Answer 1

Hint: Suppose a general point on the given line by equating the whole equation to a constant ‘k’. Now find the direction ratios of the perpendicular line on the given line with the help of supposed general point and given point in the question. Now, use the condition for two lines to be perpendicular that is given as
\[{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}=0\].

Complete step-by-step answer:

Here, we have an equation of a line and we need to determine the value of \[\beta \], if the perpendicular distance of the line from a point \[\left( \beta ,0,\beta \right)\]is \[\dfrac{\sqrt{3}}{2}\]. And we know the general equation of a line can be given by relation,
\[\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{z-{{z}_{1}}}{c}-(i)\]
Where a, b, c are direction ratios of the line and \[\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\]is a point passing through it.
We have equation of the line in problem: -
\[\dfrac{x}{1}=\dfrac{y-1}{0}=\dfrac{z+1}{-1}-(ii)\]
Now, write the given equation of the line in equation (ii) by comparing it with the general equation of the line given in equation (i); so, we get
\[\dfrac{x-0}{1}=\dfrac{y-1}{0}=\dfrac{z-\left( -1 \right)}{-1}\]
Now let the above equal terms be a number ‘k’, so we can find a general point on this line. So, we can write
\[\dfrac{x-0}{1}=\dfrac{y-1}{0}=\dfrac{z-\left( -1 \right)}{-1}=k\]
Now, equate the first three terms to ‘k’ for getting values of x, y, z in terms of k. So, we get
\[\begin{align}
  & \dfrac{x-0}{1}=k,\dfrac{y-1}{0}=k,\dfrac{z-\left( -1 \right)}{-1}=k \\
 & x-0=k,y-1=0,z-\left( -1 \right)=-k \\
 & x=k,y=1,z=-k-1(iii) \\
\end{align}\]
Hence, any general point on the given life can be as (k, 1, -k-1).
Now, we can draw a diagram as

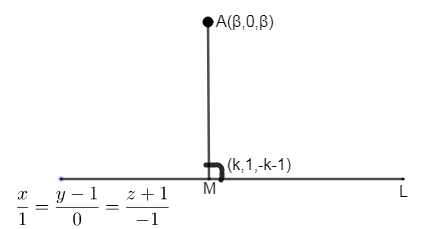
Let the point of contact of the perpendicular from point \[\left( \beta ,0,\beta \right)\] be \[\left( k,1,-k-1 \right)\]. So, we observe that line ‘L’ (given line) and line AM are perpendicular from the given diagram.
We know the condition for two lines to be perpendicular can be given as
\[{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}=0\]- (iv)
Where \[\left( {{A}_{1}},{{B}_{1}},{{C}_{1}} \right)\]and \[\left( {{A}_{2}},{{B}_{2}},{{C}_{2}} \right)\]are direction ratios of both the lines.
Now, first we can calculate direction ratios of the line AM and hence, apply the relation of equation (iv) as both the lines in the diagram are perpendicular to each other.
We know the direction ratio of a line can be calculated, if two points on the line are given as \[\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\]and \[\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)\]: -
Direction ratios = \[\left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} \right)\]
\[\Rightarrow \left( {{x}_{1}}-{{x}_{2}},{{y}_{1}}-{{y}_{2}},{{z}_{1}}-{{z}_{2}} \right)\]
So, direction ratio of AM can be given as
Direction ratios of AM = \[\left( k-\beta ,1-0,-k-1-\beta \right)\]
\[=\left( k-\beta ,1,-k-1-\beta \right)\]
Now, we know the direction ratios of line L and line AM as (1, 0, -1) and \[\left( k-\beta ,1,-k-1-\beta \right)\]. So, we can apply relation (iv) and hence, we get
\[\begin{align}
  & \left( k-\beta \right)1+1\left( 0 \right)+\left( -k-1-\beta \right)\left( -1 \right)=0 \\
 & k-\beta +0+k+1+\beta =0 \\
 & 2k+1=0 \\
 & k=\dfrac{-1}{2}-(v) \\
\end{align}\]
Hence, point ‘M’ can be given as (k, 1, -k-1). So, we get coordinates of M by putting \[k=\dfrac{-1}{2}\]from equation (v) as
Point M = \[\left( \dfrac{-1}{2},1,-\left( \dfrac{-1}{2} \right)-1 \right)\]
\[\begin{align}
  & =\left( \dfrac{-1}{2},1,\dfrac{1}{2}-1 \right) \\
 & =\left( \dfrac{-1}{2},1,\dfrac{-1}{2} \right) \\
\end{align}\]
Now, we can get perpendicular distance from point \[\left( \beta ,0,\beta \right)\]to the line by calculating the distance between A and M by simply using the distance formula.
Distance formula can be given for two points \[\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\]and \[\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)\]as
Distance =\[\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}+{{\left( {{z}_{1}}-{{z}_{2}} \right)}^{2}}}\].
Hence, distance between point A and M be
\[\begin{align}
  & AM=\sqrt{{{\left( \beta -\left( \dfrac{-1}{2} \right) \right)}^{2}}+{{\left( 0-1 \right)}^{2}}+{{\left( \beta +\dfrac{1}{2} \right)}^{2}}} \\
 & AM=\sqrt{{{\left( \beta +\dfrac{1}{2} \right)}^{2}}+{{1}^{2}}+{{\left( \beta +\dfrac{1}{2} \right)}^{2}}} \\
\end{align}\]
Now apply \[{{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\]to the above expression to simplify it further: -
\[\begin{align}
  & AM=\sqrt{{{\beta }^{2}}+\dfrac{1}{4}+\beta +1+{{\beta }^{2}}+\dfrac{1}{4}+\beta } \\
 & AM=\sqrt{2{{\beta }^{2}}+2\beta +\dfrac{3}{2}} \\
\end{align}\]
Now, it is already given in the question that perpendicular distance from point \[A\left( \beta ,0,\beta \right)\]to the line is \[\sqrt{\dfrac{3}{2}}\], hence we can put value of \[AM=\sqrt{\dfrac{3}{2}}\]in the above equation.
Hence, we get
\[\sqrt{\dfrac{3}{2}}=\sqrt{2{{\beta }^{2}}+2\beta +\dfrac{3}{2}}\]
Now, square both the sides to simplify it further. So, we get
\[\begin{align}
  & \dfrac{3}{2}=2{{\beta }^{2}}+2\beta +\dfrac{3}{2} \\
 & \Rightarrow 2{{\beta }^{2}}+2\beta =0 \\
 & 2\beta \left( \beta +1 \right)=0 \\
\end{align}\]
Hence, we get
\[\beta \] = 0 or \[\beta \] + 1 = 0
\[\beta \] = 0 or \[\beta \] = -1
Now, it is given in the question that, \[\beta \ne 0\]. Hence the value of \[\beta \] is -1.
So, option (a) is correct.

Note: One may use formula of perpendicular distance of a point by line as \[\left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+d}{\sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}} \right|\], which is wrong. This formula is used for calculating the perpendicular distance of a point from a 3 – D plane not a line. So, don’t get confused with it as well.
Relation \[{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}=0\] for two perpendiculars can be proved by dot product of two vectors i.e. \[\overrightarrow{A}.\overrightarrow{B}=\left| A \right|\left| B \right|\cos \theta \] . Hence, if direction ratio of lines in vector form is given as
\[\begin{align}
  & \overrightarrow{A}={{A}_{1}}i+{{B}_{1}}j+{{C}_{1}}k \\
 & \overrightarrow{B}={{A}_{2}}i+{{B}_{2}}j+{{C}_{2}}k \\
 & \left| A \right|\left| B \right|\cos {{90}^{\circ }}=\left( {{A}_{1}}i+{{B}_{1}}j+{{C}_{1}}k \right).\left( {{A}_{2}}i+{{B}_{2}}j+{{C}_{2}}k \right) \\
 & 0={{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}} \\
\end{align}\]
Hence proved.
Another approach would be that we can suppose point of contact of perpendicular with line as \[\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\]and satisfy it with the line and hence calculate the perpendicular length.