Question

If the length and height of a brick increases by 10 % each respectively and the breadth reduces by 20 %, what is the percentage change in the volume of the brick?
(a) 2.8
(b) 3.0
(c) 3.2
(d) 3.6

Answer 1

Hint:After the given conditions on the new dimensions, the new dimensions will be \[\dfrac{11l}{10},\dfrac{8b}{10},\dfrac{11h}{10}.\] Then find the original volume using the formula \[length\times breadth\times height.\] After that, find the change in volume and then use the formula, \[\dfrac{Change}{Original}\times 100\]%.

Complete step by step answer:
In this question, we are said that if the length and height of the brick are increased by 10 % and the breadth is reduced by 20 %, then we have to find the volume change in the brick. So, before proceeding, we want to clarify that the shape of a brick is in the form of a cuboid and the volume of the cuboid is \[l\times b\times h\] where l is length, b is the breadth, and h is height.

Now, here in this question, we get to know that the dimensions of the brick are changed a bit. According to the question, it is said that the length is increased by 10 % or we can say it as if the original length is l, then the new length is \[l+\dfrac{10}{100}l\text{ or }\dfrac{11l}{10}.\]
Now, similarly for the height which is increased by 10 % or we can say it as if the original height is h, then the new height is \[h+\dfrac{10}{100}h\text{ or }\dfrac{11h}{10}.\]
And finally for the breadth which is decreased by 20 % or we can say it as if the original breadth is b then the new breadth is \[b-\dfrac{20}{100}b\text{ or }\dfrac{8}{10}b.\]
The new dimensions of the brick are \[\dfrac{11l}{10},\dfrac{11h}{10}\text{ and }\dfrac{8b}{10}.\]

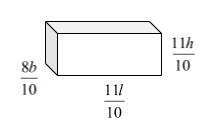
The volume of the new brick with the new dimension is \[\dfrac{11l}{10}\times \dfrac{11h}{10}\times \dfrac{8b}{10}.\]
We get,
\[\dfrac{968lbh}{1000}\]
The new volume of the brick is \[\dfrac{968lbh}{1000}.\] The original volume of the brick was lbh.
So, we can say that the change in the volume is \[lbh-\dfrac{968lbh}{1000}\text{ or }\dfrac{32}{1000}lbh.\]
The percentage in change, we will find out using the formula, \[\dfrac{Change}{Original}\times 100\]%.
Here, the change is \[\dfrac{32}{1000}lbh\] and the original is lbh. So, the percent change is,
\[\dfrac{\dfrac{32}{1000}lbh}{lbh}\times 100\]%
= 3.2 %
So, the correct option is (c).
Note:
The percentage change is of two types – percentage increase and percentage decrease. Their percent can be found out by first finding the amount increased or decreased and then divide it by original value and multiply it by 100 %.