
If the length and breadth of a rectangular field are increased, the area increases by 50%. If the increase in length was 20%, by what percentage was the breadth increased?
(a) 20%
(b) 25%
(c) 30%
(d) Data inadequate
Answer
571.8k+ views
Hint: The most important formulae for solving the question are as follows
The formula to find the % change in a quantity is as follows:
\[\Rightarrow \%change=\dfrac{new\ value-old\ value}{old\ value}\times 100\]
The formula to find the area of a rectangle is \[A=l\cdot b\] , where l is the length of the rectangular field and b is the breadth of the rectangular field. For such a question, we will first find the original area of the field. Then we will find the new length or new breadth of the field whichever is given and then we will find the new value of the other one which is not given to us or which is asked.
Complete step-by-step answer:
In this question, we are given that the area of a rectangle field is increased by 50% and that in this process, the length of this field is increased by 20%. Now, we are asked to find the % by which the breadth of this field is increased.
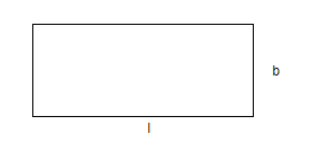
Now, we know that the area of a rectangle is given as follows:
\[A=l\cdot b\]
(Where l is the length of the rectangular field and b is the breadth of the rectangular field)
Now, as the area of this field is increased by 50%, the new area of the field that we get is as follows
\[\begin{align}
& \Rightarrow {A}'=A+50\%A \\
& \Rightarrow {A}'=A+\dfrac{50}{100}\times A \\
& \Rightarrow {A}'=A+\dfrac{1}{2}\times A \\
& \Rightarrow {A}'=\dfrac{3A}{2} \\
\end{align}\]
Now, we also know that the length of this new field is increased by 20% and the new length of the field that we get is as follows
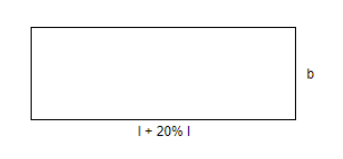
\[\begin{align}
& \Rightarrow {l}'=l+20\%l \\
& \Rightarrow {l}'=l+\dfrac{20}{100}\times l \\
& \Rightarrow {l}'=l+\dfrac{1}{5}\times l \\
& \Rightarrow {l}'=\dfrac{6l}{5} \\
\end{align}\]
Now, for calculating the area of the new field that is given as follows
\[\Rightarrow {A}'={l}'\cdot {b}'\]
Now, putting the values of \[{A}'\ and\ {l}'\] in terms of A and l respectively, we can write as follows
\[\begin{align}
& \Rightarrow {A}'={l}'\cdot {b}' \\
& \Rightarrow \dfrac{3A}{2}=\dfrac{6l}{5}\cdot {b}' \\
\end{align}\]
Now, originally, we know that \[A=l\cdot b\] , hence, we can write the following equation using the above information as follows
\[\begin{align}
& \Rightarrow \dfrac{3l\cdot b}{2}=\dfrac{6l}{5}\cdot {b}' \\
& \Rightarrow \dfrac{b}{2}=\dfrac{2}{5}\cdot {b}' \\
& \Rightarrow \dfrac{5b}{4}={b}' \\
\end{align}\]
Now, we get that the value of the breadth ‘b’ of the field has become \[\dfrac{5b}{4}\] , so we can calculate the % change in the value of the breadth as follows
\[\begin{align}
& \Rightarrow \%change=\dfrac{new\ value-old\ value}{old\ value}\times 100 \\
& \Rightarrow \%change=\dfrac{\dfrac{5b}{4}-b}{b}\times 100 \\
& \Rightarrow \%change=\dfrac{\dfrac{b}{4}}{b}\times 100 \\
& \Rightarrow \%change=\dfrac{1}{4}\times 100 \\
& \Rightarrow \%change=25\% \\
\end{align}\]
Hence, we get that the breadth of the rectangular field increased by 25%.
Note: It is very important for the students to know the % change formula because without knowing it, one can never get to the correct answer which is given as follows
\[\Rightarrow \%change=\dfrac{new\ value-old\ value}{old\ value}\times 100\]
If they take the denominator as the new value, then the result will be different. Also, it is important for the students to remember the area of a rectangle to get to the correct answer. The students can make an error if they directly take the obtained value of the new breadth of the new rectangular field as the change that is added in the original breadth. They should know that what they have obtained is the total changed breadth of the field rather than being just the change in the original one.
The formula to find the % change in a quantity is as follows:
\[\Rightarrow \%change=\dfrac{new\ value-old\ value}{old\ value}\times 100\]
The formula to find the area of a rectangle is \[A=l\cdot b\] , where l is the length of the rectangular field and b is the breadth of the rectangular field. For such a question, we will first find the original area of the field. Then we will find the new length or new breadth of the field whichever is given and then we will find the new value of the other one which is not given to us or which is asked.
Complete step-by-step answer:
In this question, we are given that the area of a rectangle field is increased by 50% and that in this process, the length of this field is increased by 20%. Now, we are asked to find the % by which the breadth of this field is increased.

Now, we know that the area of a rectangle is given as follows:
\[A=l\cdot b\]
(Where l is the length of the rectangular field and b is the breadth of the rectangular field)
Now, as the area of this field is increased by 50%, the new area of the field that we get is as follows
\[\begin{align}
& \Rightarrow {A}'=A+50\%A \\
& \Rightarrow {A}'=A+\dfrac{50}{100}\times A \\
& \Rightarrow {A}'=A+\dfrac{1}{2}\times A \\
& \Rightarrow {A}'=\dfrac{3A}{2} \\
\end{align}\]
Now, we also know that the length of this new field is increased by 20% and the new length of the field that we get is as follows
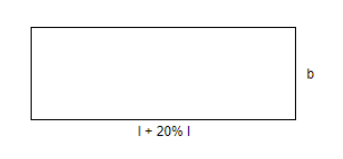
\[\begin{align}
& \Rightarrow {l}'=l+20\%l \\
& \Rightarrow {l}'=l+\dfrac{20}{100}\times l \\
& \Rightarrow {l}'=l+\dfrac{1}{5}\times l \\
& \Rightarrow {l}'=\dfrac{6l}{5} \\
\end{align}\]
Now, for calculating the area of the new field that is given as follows
\[\Rightarrow {A}'={l}'\cdot {b}'\]
Now, putting the values of \[{A}'\ and\ {l}'\] in terms of A and l respectively, we can write as follows
\[\begin{align}
& \Rightarrow {A}'={l}'\cdot {b}' \\
& \Rightarrow \dfrac{3A}{2}=\dfrac{6l}{5}\cdot {b}' \\
\end{align}\]
Now, originally, we know that \[A=l\cdot b\] , hence, we can write the following equation using the above information as follows
\[\begin{align}
& \Rightarrow \dfrac{3l\cdot b}{2}=\dfrac{6l}{5}\cdot {b}' \\
& \Rightarrow \dfrac{b}{2}=\dfrac{2}{5}\cdot {b}' \\
& \Rightarrow \dfrac{5b}{4}={b}' \\
\end{align}\]
Now, we get that the value of the breadth ‘b’ of the field has become \[\dfrac{5b}{4}\] , so we can calculate the % change in the value of the breadth as follows
\[\begin{align}
& \Rightarrow \%change=\dfrac{new\ value-old\ value}{old\ value}\times 100 \\
& \Rightarrow \%change=\dfrac{\dfrac{5b}{4}-b}{b}\times 100 \\
& \Rightarrow \%change=\dfrac{\dfrac{b}{4}}{b}\times 100 \\
& \Rightarrow \%change=\dfrac{1}{4}\times 100 \\
& \Rightarrow \%change=25\% \\
\end{align}\]
Hence, we get that the breadth of the rectangular field increased by 25%.
Note: It is very important for the students to know the % change formula because without knowing it, one can never get to the correct answer which is given as follows
\[\Rightarrow \%change=\dfrac{new\ value-old\ value}{old\ value}\times 100\]
If they take the denominator as the new value, then the result will be different. Also, it is important for the students to remember the area of a rectangle to get to the correct answer. The students can make an error if they directly take the obtained value of the new breadth of the new rectangular field as the change that is added in the original breadth. They should know that what they have obtained is the total changed breadth of the field rather than being just the change in the original one.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




