Question

If the intercept made by the line between the axis is bisected at the point $\left( {5,2} \right)$, then it’s equation is
1)$5x + 2y = 20$
2)$2x + 5y = 20$
3)$5x - 2y = 20$
4)$2x - 5y = 20$

Answer 1

Hint: Given to us is the midpoint of a line that intercepts the axes. So, we can find the points where the line intersects the axis using the midpoint formula, as in the points of the intercepts in the axis have only the x-coordinate or y-coordinate. So, we will have two points that lie on a line, we can easily use the two point formula of a line to find the equation of the line.

Complete step-by-step solution:
The given point that bisects the line is $\left( {5,2} \right)$.
Let the points where it intersects the x-axis and y-axis be $\left( {x,0} \right)$ and $\left( {0,y} \right)$ respectively.

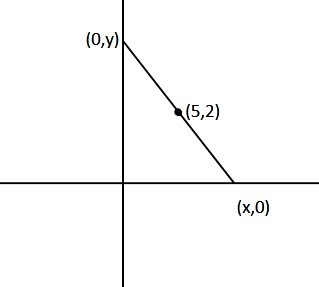
[Since, in the x-axis the y-coordinate will be $0$ and in the y-axis x-coordinate will be $0$]
The midpoint formula is,
$m\left( {\alpha ,\beta } \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
Where, $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the two points of the line, whose mid-point is $m\left( {\alpha ,\beta } \right)$.
Therefore, here, $m\left( {\alpha ,\beta } \right) = \left( {5,2} \right)$, $\left( {{x_1},{y_1}} \right) = \left( {x,0} \right)$, $\left( {{x_2},{y_2}} \right) = \left( {0,y} \right)$.
Therefore, substituting the points in the given formula, we get,
$\left( {5,2} \right) = \left( {\dfrac{{x + 0}}{2},\dfrac{{0 + y}}{2}} \right)$
$ \Rightarrow \left( {5,2} \right) = \left( {\dfrac{x}{2},\dfrac{y}{2}} \right)$
Comparing the x-coordinate and y-coordinate on both sides of the equality, we get,
$\dfrac{x}{2} = 5$
$ \Rightarrow x = 10$
And, $\dfrac{y}{2} = 2$
$ \Rightarrow y = 4$
Therefore, the two points where the line intersects the axes is $\left( {10,0} \right)$ and $\left( {0,4} \right)$.
Therefore, we have two points of a line.
So, we can find the equation of the line by using the formula,
$\dfrac{{y - {y_1}}}{{x - {x_1}}} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Here, $\left( {{x_1},{y_1}} \right) = \left( {10,0} \right)$ and $\left( {{x_2},{y_2}} \right) = \left( {0,4} \right)$.
Substituting the values, we get,
$\dfrac{{y - 0}}{{x - 10}} = \dfrac{{4 - 0}}{{0 - 10}}$
$ \Rightarrow \dfrac{y}{{x - 10}} = \dfrac{4}{{ - 10}}$
Simplifying the right hand side, we get,
$ \Rightarrow \dfrac{y}{{x - 10}} = \dfrac{2}{{ - 5}}$
Now, cross multiplying, we get,
$ \Rightarrow - 5y = 2\left( {x - 10} \right)$
$ \Rightarrow - 5y = 2x - 20$
Adding $5y$ on both sides, we get,
$ \Rightarrow 0 = 2x + 5y - 20$
Adding, $20$ on both sides, we get,
$ \Rightarrow 20 = 2x + 5y$
Now, changing the sides, we get,
$ \Rightarrow 2x + 5y = 20$
Therefore, the equation of the line is, $2x + 5y = 20$, the correct option is 2.

Note: We can also solve this problem by finding the slope of the line from any two of the points, either be the midpoint and any intercept or be the two intercepts. And, then using the slope-point formula to get the required answer, the formula is,
$\dfrac{{y - {y_1}}}{{x - {x_1}}} = m$.