Question

If the incentre of an equilateral triangle is (1, 1) and the equation of its one side is 3x + 4y + 3 = 0, then find the equation of the circumcircle of this triangle.
(a) ${{x}^{2}}+{{y}^{2}}-2x-2y-2=0$
(b) ${{x}^{2}}+{{y}^{2}}-2x-2y-14=0$
(c) ${{x}^{2}}+{{y}^{2}}-2x-2y+2=0$
(d) ${{x}^{2}}+{{y}^{2}}-2x-2y+14=0$

Answer 1

Hint:Note that for an equilateral triangle, circumcentre and incentre coincide. So, circumcentre is (1, 1). Find the inradius. Use this and the figure to get the expression $\sin 30{}^\circ =\dfrac{1}{2}=\dfrac{2}{R}$. This gives R = 4. Now, we have the centre and the radius of the circumcentre. Using these find the equation of the circumcircle of this triangle.

Complete Step-by-step answer:
In this question, we are given that the incentre of an equilateral triangle is (1, 1) and the equation of its one side is 3x + 4y + 3 = 0.
Using this information, we need to find the equation of the circumcircle of this triangle.
First, let us define the incentre and circumcentre.
The incentre of a triangle may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, and as the centre point of the inscribed circle of the triangle.
The circumcentre of a triangle is defined as the point where the perpendicular bisectors of the sides of that particular triangle intersect. In other words, the point of concurrency of the bisector of the sides of a triangle is called the circumcentre.
We know that, for an equilateral triangle, circumcentre and incentre coincide.
Using this property, the circumcentre of the given triangle is (1, 1). …(1)
In the shown figure, R is the circumradius of the triangle.
r is the inradius of the triangle.
The shown angle is $30{}^\circ $.

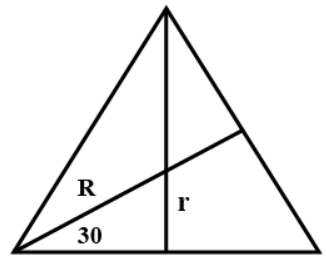
Now, the inradius, r is the distance of (1,1) from the line 3x + 4y + 3 = 0
So, inradius, r $=\dfrac{|3\cdot 1+4\cdot 1+3|}{\sqrt{{{3}^{2}}+{{4}^{2}}}}=2$
Now, $\sin 30{}^\circ =\dfrac{1}{2}=\dfrac{r}{R}$
$\sin 30{}^\circ =\dfrac{1}{2}=\dfrac{2}{R}$
R = 4
Hence, the circumradius, R = 4 units.
Now, we know that general equation of circle is: \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] with centre at $\left( -g,-f \right)$ and radius = $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.
Now the circumcircle has its centre at (1, 1) and has the radius R = 4 units. We will substitute these values in the general equation above. So, the equation of the circumcircle is:
${{x}^{2}}+{{y}^{2}}-2x-2y-14=0$
So, option (b) is correct.

Note:It is important to know the following: the incentre of a triangle may be equivalently defined as the point where the internal angle bisectors of the triangle cross and that for an equilateral triangle, circumcentre and incentre coincide.