Question

If the hypotenuse of a right-angled triangle is 5cm and its remaining sides are in the ratio of 1:2, then find the lengths of its sides?

Answer 1

Hint: We start solving the problem by assigning the variables for the lengths of the remaining two sides of the right-angled triangle. We then recall the Pythagoras theorem as the square of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. We use this definition and make the necessary calculations to get the values of the required lengths of the other two sides.

Complete step-by-step solution
According to the problem, we are given that the hypotenuse of a right-angled triangle is 5cm and its remaining sides are in the ratio of 1:2. We need to find the length of the remaining two sides.
Let us assume the remaining two sides are x, 2x.

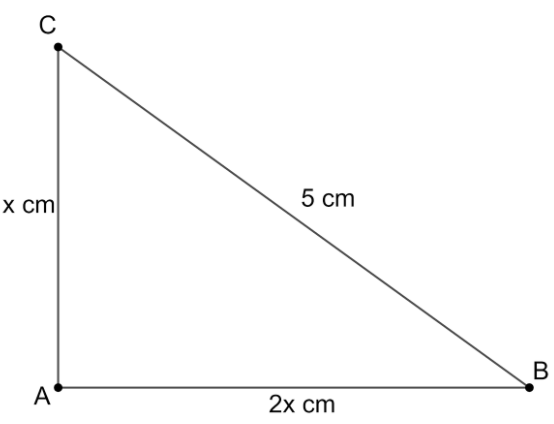
From the Pythagoras theorem, we know that the square of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
So, we have ${{5}^{2}}={{x}^{2}}+{{\left( 2x \right)}^{2}}$.
$\Rightarrow 25={{x}^{2}}+4{{x}^{2}}$.
$\Rightarrow 25=5{{x}^{2}}$.
$\Rightarrow 5={{x}^{2}}$.
$\Rightarrow x=\sqrt{5}$cm.
So, we have length if one of the remaining sides is $\sqrt{5}$ cm.
Now, let us find the length of the other side.
So, the length of the other side is $2x=2\sqrt{5}$ cm.
$\therefore$ The lengths of the remaining sides are $\sqrt{5}$ cm and $2\sqrt{5}$ cm.

Note: Whenever we get this type of problem, we try to start solving by assigning the variables for the unknowns present in the problem. We should know that hypotenuse is the largest side of the Right-angled triangle. We can also find the values of the angles present in the triangle using the lengths of the sides obtained. Similarly, we can expect problems to find the area of the triangle.