Question

If the function $f\left( x \right)={{\log }_{2}}\left( {{\log }_{3}}\left( {{\log }_{\dfrac{1}{2}}}\left( \cos x+a \right) \right) \right)$ has a first derivative $\forall x\in R$. Find the interval in which ‘a’ exists.
(a) $a\in \left( 1,\dfrac{3}{2} \right)$.
(b) $a\in \left( \dfrac{1}{2},1 \right)$.
(c) $a\in \left( 1,\dfrac{5}{2} \right)$.
(d) $a\in \left\{ \phi \right\}$.

Answer 1

Hint: We need to find the interval for ‘a’, so that f(x) has a first derivative. We use the fact that logarithmic function ${{\log }_{b}}\left( y \right)$ for any value of b>0 if and only if $y>0$. We have three logarithmic functions here and we apply this for each logarithmic function. After applying we get three different feasible intervals for ‘a’, we will take intersection to get the required interval for ‘a’.

Complete step-by-step solution:
Given that we have a function $f\left( x \right)={{\log }_{2}}\left( {{\log }_{3}}\left( {{\log }_{\dfrac{1}{2}}}\left( \cos x+a \right) \right) \right)$ and first derivative exists for f(x) $\forall x\in R$. We need to find the value of ‘a’ so, that derivative exists.
To find the value of ‘a’, we first need to know that derivative ${{\log }_{b}}\left( y \right)$ exists for any value of b>0 if and only if $y>0$.
We use this to find the value of ‘a’. Let us assume $y={{\log }_{3}}\left( {{\log }_{\dfrac{1}{2}}}\left( \cos x+a \right) \right)$, $z={{\log }_{\dfrac{1}{2}}}\left( \cos x+a \right)$ and $r=\left( \cos x+a \right)$.
So, we have and derivative of f(x) exists if and only if $y>0$.
${{\log }_{3}}\left( {{\log }_{\dfrac{1}{2}}}\left( \cos x+a \right) \right)>0$.
We know that if ${{\log }_{b}}\left( x \right)=y$, then $x={{b}^{y}}$.
${{\log }_{\dfrac{1}{2}}}\left( \cos x+a \right)> {{3}^{0}}$.
${{\log }_{\dfrac{1}{2}}}\left( \cos x+a \right)> 1$.
We know that ${{\log }_{\dfrac{1}{b}}}\left( y \right)=-{{\log }_{b}}\left( y \right)$.
$-{{\log }_{2}}\left( \cos x+a \right)> 1$.
${{\log }_{2}}\left( \cos x+a \right)< -1$.
$\cos x+a< {{2}^{-1}}$
$\cos x+a< \dfrac{1}{2}$.
$a<\dfrac{1}{2}-\cos x$ ------------(1).
We know that the value of -$\cos x$ for $\forall x\in R$ lies in $\left[ -1,1 \right]$.
So, $\dfrac{1}{2}-\cos x\in \left[ \dfrac{1}{2}-1,\dfrac{1}{2}+1 \right]$.
$\dfrac{1}{2}-\cos x\in \left[ \dfrac{-1}{2},\dfrac{3}{2} \right]$.
From equation (1), we can see that the value of ‘a’ must be less than the function $\dfrac{1}{2}-\cos x$ for any given value of x. This will be possible only if the value of a is less than the minimum of the function $\dfrac{1}{2}-\cos x$. So, ‘a’ must be less than $\dfrac{-1}{2}$ in order to be less than the function $\dfrac{1}{2}-\cos x$ at any value of x.
We have got $a <\dfrac{-1}{2}$ -----------(2).
Now we have function $y={{\log }_{3}}\left( z \right)$ and derivative of ‘y’ exists only if $z>0$.
${{\log }_{\dfrac{1}{2}}}\left( \cos x+a \right)> 0$.
We know that ${{\log }_{\dfrac{1}{b}}}\left( y \right)=-{{\log }_{b}}\left( y \right)$.
$-{{\log }_{2}}\left( \cos x+a \right)> 0$.
${{\log }_{2}}\left( \cos x+a \right)< 0$.
$\cos x+a< {{2}^{0}}$.
$\cos x+a< 1$.
$a<1-\cos x$ ------------(3).
We know that the value of -$\cos x$ for $\forall x\in R$ lies in $\left[ -1,1 \right]$.
So, $1-\cos x\in \left[ 1-1,1+1 \right]$.
$1-\cos x\in \left[ 0,2 \right]$.
From equation (3), we can see that the value of ‘a’ must be less than the function $1-\cos x$ for any given value of x. This will be possible only if the value of a is less than the minimum of the function $1-\cos x$. So, ‘a’ must be less than 0 in order to be less than the function $1-\cos x$ at any value of x.
We have got an interval for ‘a’ as $a< 0$ ------------(4).
Now we have function \[z={{\log }_{\dfrac{1}{2}}}\left( r \right)\] and derivative of ‘z’ exists only if $r >0$.
$\cos x+a > 0$.
$a> -\cos x$ -----------(5).
We know that the value of -$\cos x$ for $\forall x\in R$ lies in $\left[ -1,1 \right]$.
From equation (5), we can see that the value of ‘a’ must be greater than the function $-\cos x$ for any given value of x. This will be possible only if the value of a is greater than the maximum of the function $-\cos x$. So, ‘a’ must be greater than 1 in order to be greater than the function $-\cos x$ at any value of x.
We have got an interval for ‘a’ as $a >1$ ---------(6).
To find the common interval for ‘a’, we need to find intersection from equations (2), (4), and (6).
The interval of ‘a’ is $\left( a< \dfrac{-1}{2} \right)\cap \left( a< 0 \right)\cap \left( a> 1 \right)$.
Let us draw all three intervals on the number line.

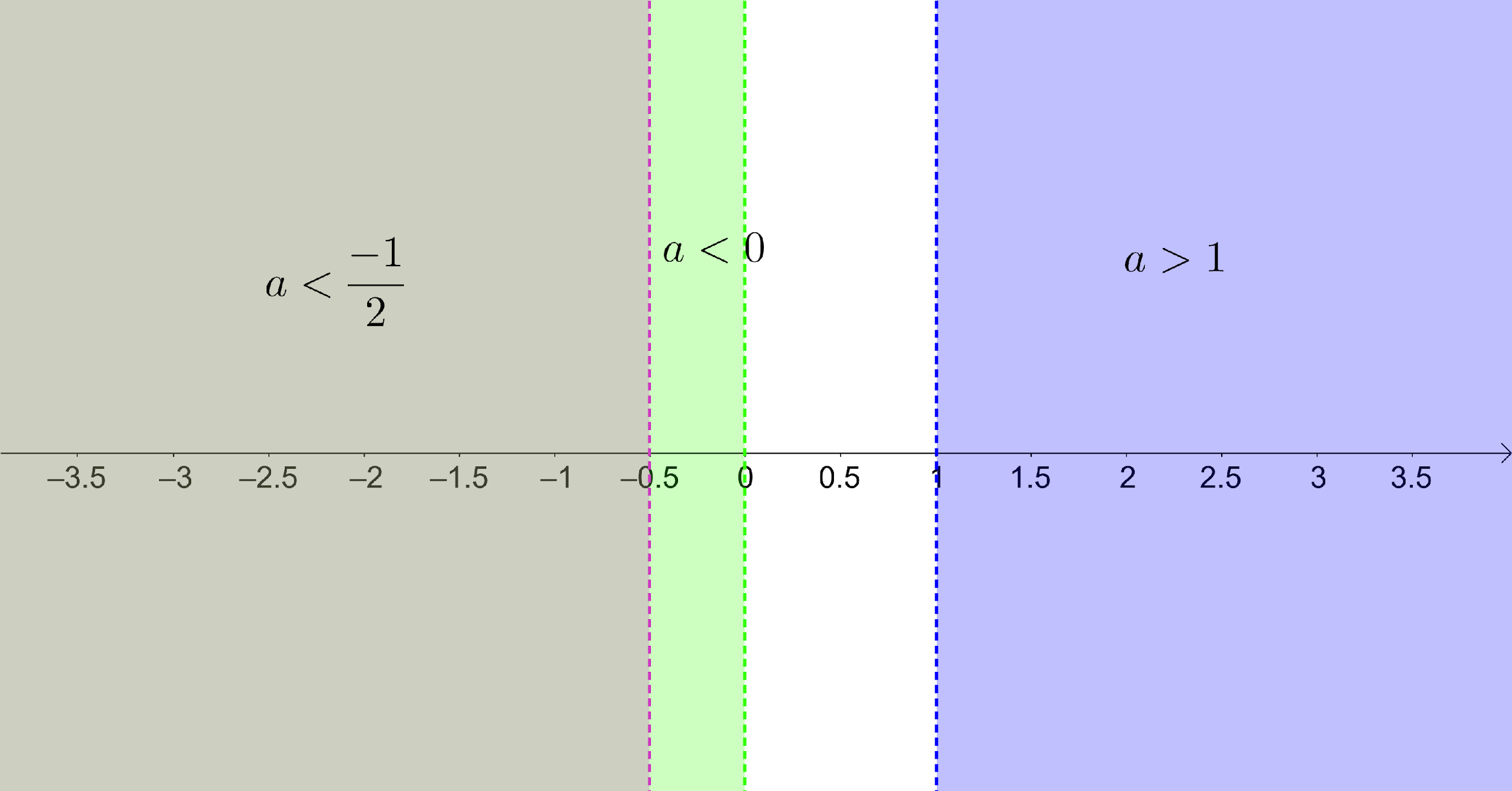
If we look for common intervals in the number line, we don’t final any intersection between all the three intervals. This makes our solution set a null set. $a< \dfrac{-1}{2}$ and $a< 0$ has an intersection but we have to see the interval where all the three intervals have a common intersection.
$\therefore$ The interval for a is $a\in \left\{ \phi \right\}$.
The correct option is (d).

Note: If we have situation like $a< \left[ {{x}_{1}},{{x}_{2}} \right]$, then we need to consider the values which are less than ${{x}_{1}}$ for a. If we have situation like $a >\left[ {{x}_{1}},{{x}_{2}} \right]$, then we need to consider the values which are greater than ${{x}_{1}}$ for ‘a’. We should always take the intersection if two or more different intervals are occurring for ‘a’.