Question

If the focus of a parabola is $\left( { - 2,1} \right)$ and the directrix has the equation $x + y = 3$ , then the vertex is

A.(0, 3)
B. $\left( { - 1,\,\dfrac{1}{2}} \right)$
C.(−1, 2)
D.(2, −1)

Answer 1

Hint: The axis of the parabola is perpendicular to the directrix and passes through both the vertex and the focus. The equation of the directrix and the coordinates of the focus is given. Hence one can easily find the equation of the axis of the parabola.
Next, find the vertex (Note that vertex is the midpoint of the foot of directrix and focus).

Complete step-by-step answer:
Given, the focus of the parabola is at $\left( { - 2,1} \right)$ and the equation of directrix is given by $x + y = 3$
Now, the slope of a line perpendicular to the directrix $x + y = 3$, is 1
Since the axis of the parabola is perpendicular to the directrix, the equation of the axis is $x - y = c$ , say.
Since the axis passes through the focus $\left( { - 2,1} \right)$ , we substitute \[\;x = - 2,{\text{ }}y = 1\] in the equation $x - y = c$
$
   \Rightarrow - 2 - 1 = c \\
   \Rightarrow c = - 3 \\
 $
Therefore, The equation of the axis of the parabola is $x - y = - 3$
Now, solving the equations of the directrix and the axis, we get

\[
  \,\,\,\,\,\,\,\,\,x + y = 3 \\
  \left( + \right)x - y = - 3 \\
 \]
 We get, \[2x = 0\]
 $ \Rightarrow x = 0$
 On substituting value of x in $x + y = 3$, we get
\[ \Rightarrow 0 + y = 3\]
 $ \Rightarrow y = 3$
 Therefore, the foot of the directrix is (0, 3)

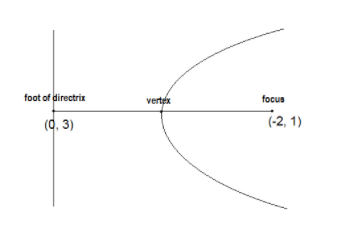
Again, we know that vertex is the midpoint of the foot of the directrix and focus.
 Therefore, vertex ≡$\left( {\dfrac{{0 - 2}}{2},\,\dfrac{{3 + 1}}{2}} \right) = \left( { - 1,\,\,2} \right)$
 Hence, If the focus of a parabola is $\left( { - 2,1} \right)$ and the directrix has the equation $x + y = 3$ , then the vertex is at $\left( { - 1,\,\,2} \right)$
Therefore, the correct option is (C).

Note: A parabola is a curve where any point is at an equal distance from: a fixed point (the focus), and. a fixed straight line (the directrix).
 Note that, the axis of the parabola is perpendicular to the directrix and passes through both the vertex and the focus.
Also, vertex is the midpoint of the foot of the directrix and focus.