Question

If the diagonals of a rhombus are $24dm$ and $10dm$ then the perimeter of rhombus will be
(A) $68dm$
(B) $60dm$
(C) $52dm$
(D) $50dm$

Answer 1

Hint: For finding the perimeter of a rhombus we should multiply the length of a side of rhombus by 4, mathematically that can be expressed as $4\times a$ where $a$ is the length of the side of rhombus. We should determine the value of a side of rhombus using the given length of diagonals of a rhombus using the Pythagoras theorem.

Complete step by step answer:
Given in the question that the length of the diagonals of a rhombus are $24dm$ and $10dm$.
Since we know that all the sides of a rhombus are equal and the perimeter of the respective rhombus can be given by multiplying the length of a side of rhombus by 4, mathematically that can be expressed as $4\times a$ where $a$ is the length of the side of rhombus.
From a general point of view we can say that 4 right angled triangles are formed inside a rhombus by combining its sides and diagonals.

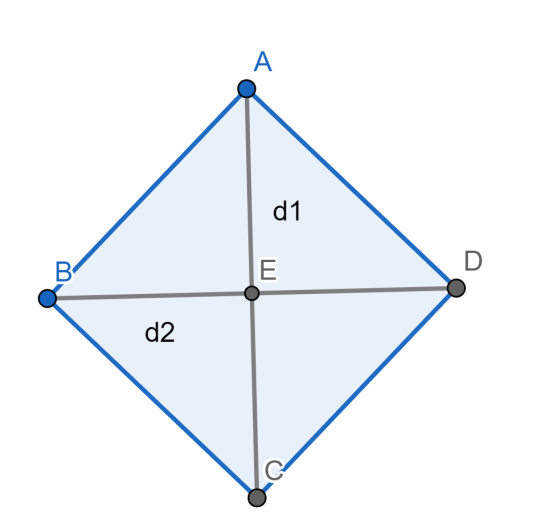
As we know from the basic concept that we have Pythagoras theorem to apply in a right angle triangle. By applying that for a rhombus we can predict the length of the side of the rhombus using the lengths of the diagonals.
As we have assumed $a$ as the length of the side of rhombus. We can assume ${{d}_{1}}$ and ${{d}_{2}}$ as the lengths of the diagonals.
By observing the diagram we have a right angle triangle $\vartriangle ABE$ and using the concept of symmetry we can say that
$a=\sqrt{{{\left( \dfrac{{{d}_{1}}}{2} \right)}^{2}}+{{\left( \dfrac{{{d}_{2}}}{2} \right)}^{2}}}$
By simplifying this $a=\dfrac{\sqrt{d_{1}^{2}+d_{2}^{2}}}{2}$
Hence, the perimeter of the rhombus is given by $4a=2\sqrt{d_{1}^{2}+d_{2}^{2}}$ .
As from the question we have the lengths of both the diagonal of the rhombus as $24dm$ and $10dm$ respectively.
Hence, we can conclude that the perimeter of the rhombus will be equal to
$\begin{align}
  & 2\sqrt{{{10}^{2}}+{{24}^{2}}} \\
 & \Rightarrow 2\sqrt{100+576} \\
 & \Rightarrow 2\sqrt{676} \\
 & \Rightarrow 2\left( 26 \right) \\
 & \Rightarrow 52 \\
\end{align}$
Hence we now end up with a conclusion that the perimeter of a rhombus having the length of the diagonals as $10dm$ and $24dm$ respectively is $52dm$ .

So, the correct answer is “Option C”.

Note: While answering questions of this type it will be efficient if we remember that the perimeter of a rhombus can be directly given by using the lengths of diagonals of the rhombus without determining the length of a side and it can be given by $2\sqrt{d_{1}^{2}+d_{2}^{2}}$. This would save our time answering questions of this model in a competitive exam as the steps are reduced.