Question

If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Answer 1

Hint – To prove it is a rectangle, we draw its diagonals and then compare the triangles formed w.r.t the diagonals. We use properties of triangles to find the angles of the figure.

Complete step-by-step answer:
Given Data, in parallelogram ABCD, AC = BD.
To prove: Parallelogram ABCD is rectangle.

Proof: Let us consider ∆ACB and ∆BDA from the figure

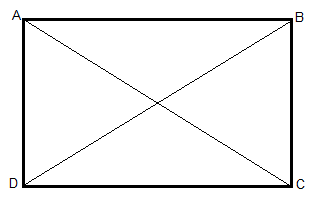
Let us compare their sides, AC = BD (given)
They have a common side, i.e. AB = BA
We know the opposite sides of a parallelogram are equal, hence BC = AD
The SSS rule states that: If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.
⟹$\Delta {\text{ACB }} \cong {\text{ }}\Delta {\text{BDA - - - (sss rule)}}$
CPCT (corresponding parts of congruent triangle) theorem states that if two or more triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also congruent to each other.
Hence from congruent triangles ∆ACB and ∆BDA,
$\therefore \angle {\text{ABC = }}\angle {\text{BAD - - - (1)}}$.

As we know opposite sides of a parallelogram are equal, applying that to the figure we get,
Now AD ∥ BC.
AD ∥ BC and they are intersected by AB which is a traversal.
From the concept of traversal we know, the sum of consecutive interior angles on the same side of traversal is$180^\circ $.
$\therefore \angle {\text{BAD + }}\angle {\text{ABC = 180}}^\circ {\text{ - - - (2)}}$

Now, comparing equations (1) and (2), we get
$\angle {\text{BAD = }}\angle {\text{ABC = 90}}^\circ $
$\therefore $$\angle {\text{A = 90}}^\circ {\text{ and }}\angle {\text{C = 90}}^\circ $
Hence the angles in the figure are 90°, i.e. the given parallelogram is a rectangle.
Note – In order to solve this type of problem the key is to use the given data in the question and draw an appropriate figure. Upon drawing the figure we use the properties of diagonals and triangles formed to prove that the angles inside the figure are 90°, to prove it as a rectangle.
In geometry, a transversal is a line that passes through two lines in the same plane at two distinct points.