Question

If the coefficient of friction between an insect and the bowl is $\mu $ and the radius of the bowl is $r$ the maximum height to which the insect can crawl in the bowl is:

Answer 1

Hint: First we will draw the free body diagram of an insect that is crawling in the bowl after doing that we will find the forces acting on the insect. By doing so we will lead to our solution.

Formula used:
${{F}_{L}}=\mu N$

Complete step by step solution:

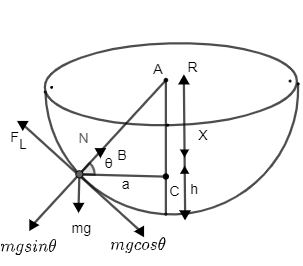
$\to $ From the figure we can give below formula
$N=mg\sin \theta ....\left( 1 \right)$
And frictional force will be equal to
${{F}_{L}}=mg\cos \theta ....\left( 2 \right)$

$\to $Now let’s divide equation (1) by equation (2) we will get
$\begin{align}
  & \dfrac{N}{{{F}_{L}}}=\dfrac{mg\sin \theta }{mg\cos \theta } \\
 & \therefore \tan \theta =\dfrac{N}{{{F}_{L}}}.....\left( 3 \right) \\
\end{align}$

$\to $From figure (1) if we consider

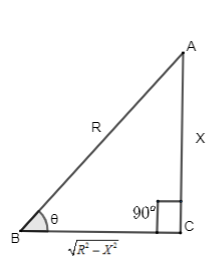
$\to $From the triangle ABC
$\begin{align}
  & \Rightarrow \tan \theta =\dfrac{AC}{BC} \\
 & \therefore \tan \theta =\dfrac{X}{\sqrt{{{R}^{2}}-{{X}^{2}}}}......(4) \\
\end{align}$

$\to $Now let’s equalize equation (3) and equation (4) we will get
$\dfrac{N}{{{F}_{L}}}=\dfrac{X}{\sqrt{{{R}^{2}}-{{X}^{2}}}}....\left( 5 \right)$

$\to $We know that frictional force
${{F}_{L}}=\mu N$
${{F}_{L}}$ = frictional force
$\mu $ = coefficient of the friction
N = normal force

$\to $Substitute value at ${{F}_{L}}$ in equation (5)
$\begin{align}
  & \Rightarrow \dfrac{N}{\mu N}=\dfrac{X}{\sqrt{{{R}^{2}}-{{X}^{2}}}} \\
 & \Rightarrow \dfrac{1}{\mu }=\dfrac{X}{\sqrt{{{R}^{2}}-{{X}^{2}}}} \\
 & \therefore X=\dfrac{\sqrt{{{R}^{2}}-{{X}^{2}}}}{\mu } \\
\end{align}$

$\to $Taking square on the both sides
$\begin{align}
  & \Rightarrow {{X}^{2}}=\dfrac{{{R}^{2}}-{{X}^{2}}}{{{\mu }^{2}}} \\
 & \Rightarrow {{\mu }^{2}}{{X}^{2}}+{{X}^{2}}={{R}^{2}} \\
 & \therefore {{X}^{2}}\left( {{\mu }^{2}}+1 \right)={{R}^{2}} \\
\end{align}$

$\to $Taking under root on the both sides we get
$X=\dfrac{R}{\sqrt{{{\mu }^{2}}+1}}....\left( 6 \right)$

$\to $Now from the figure (1) height (h) is
$h=R-X....\left( 7 \right)$

$\to $Now substitute value of x in equation (7) we get
$\begin{align}
  & \Rightarrow h=R-\dfrac{R}{\sqrt{{{\mu }^{2}}+1}} \\
 & \therefore h=R\left( 1-\dfrac{1}{\sqrt{{{\mu }^{2}}+1}} \right).....\left( 8 \right) \\
\end{align}$

$\to $Hence the height to which the insect can crawl in the bowl is given by the equation (8).

Additional information:
Definition of frictional force:
“Frictional force can be defined as the force generated by two surface that are in contact and slide against each other.”
Definition of Pseudo force:
“It is an apparent force that acts on all masses whose motion is described using a non-inertial frame of reference frame, such as a rotating reference frame.”

Note:
This question is all dependent on the free body diagram of the insect. If we make any mistake in any single force then it will lead us to the incorrect solution. So be careful when we define forces on free body diagrams.