Question

If the chord $y=mx+c$ subtends a right angle at the vertex of the parabola ${{y}^{2}}=4ax$, then the value of c is
(A) -4am
(B) 4am
(C) -2am
(D) 2am

Answer 1

Hint: We solve this question by first assuming the given chord intersects the parabola ${{y}^{2}}=4ax$ at the points $A\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $B\left( at_{2}^{2},2a{{t}_{2}} \right)$. Then we find the slopes of the lines from point A to origin and line from B to origin and use the condition that the lines with slopes ${{m}_{1}}$ and ${{m}_{2}}$are perpendicular then ${{m}_{1}}{{m}_{2}}=-1$ to find the relation between ${{t}_{1}}$ and ${{t}_{2}}$. Then we find the equation of chord AB and compare with the equation of the given chord and find the value of c.

Complete step by step answer:
We are given that the chord $y=mx+c$ of the parabola ${{y}^{2}}=4ax$ and it subtends a right angle at the vertex.
Let us assume that the chord intersects the parabola ${{y}^{2}}=4ax$ at points $A\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $B\left( at_{2}^{2},2a{{t}_{2}} \right)$.

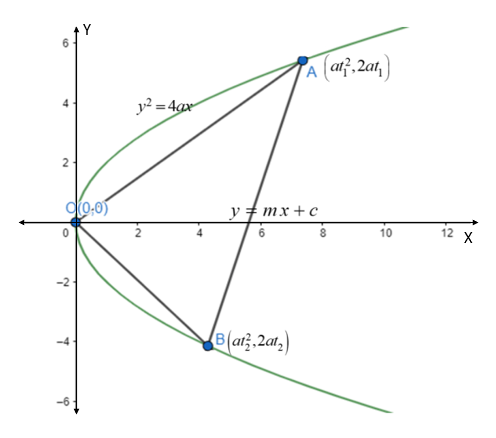
Now let us find the slope of the lines from the vertex of the parabola, that is origin to the points A and B.
Slope of the line OA is
${{m}_{1}}=\dfrac{2a{{t}_{1}}-0}{at_{1}^{2}-0}=\dfrac{2a{{t}_{1}}}{at_{1}^{2}}=\dfrac{2}{{{t}_{1}}}$
Slope of the line OB is,
${{m}_{2}}=\dfrac{2a{{t}_{2}}-0}{at_{2}^{2}-0}=\dfrac{2a{{t}_{2}}}{at_{2}^{2}}=\dfrac{2}{{{t}_{2}}}$
As we are given that the chord bisects the right angle at the vertex of the parabola, the product of the slopes of the lines from origin to A and B is -1.
$\Rightarrow {{m}_{1}}{{m}_{2}}=-1$
Substituting the values of ${{m}_{1}}$ and ${{m}_{2}}$ in the above formula we get,
$\begin{align}
  & \Rightarrow \dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1 \\
 & \Rightarrow {{t}_{1}}{{t}_{2}}=-4 \\
\end{align}$
Now let us find the equation of the chord AB.
Let us consider the formula for line joining $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is
$\left( y-{{y}_{1}} \right)=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$
Using this we can find the equation of AB as,
$\begin{align}
  & \Rightarrow \left( y-2a{{t}_{1}} \right)=\dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{at_{2}^{2}-at_{1}^{2}}\left( x-at_{1}^{2} \right) \\
 & \Rightarrow \left( y-2a{{t}_{1}} \right)=\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( t_{2}^{2}-t_{1}^{2} \right)}\left( x-at_{1}^{2} \right) \\
 & \Rightarrow \left( y-2a{{t}_{1}} \right)=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}\left( x-at_{1}^{2} \right) \\
\end{align}$
$\begin{align}
  & \Rightarrow y=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}x-\dfrac{2at_{1}^{2}}{{{t}_{2}}+{{t}_{1}}}+2a{{t}_{1}} \\
 & \Rightarrow y=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}x-\dfrac{2at_{1}^{2}-2a{{t}_{1}}\left( {{t}_{2}}+{{t}_{1}} \right)}{{{t}_{2}}+{{t}_{1}}} \\
\end{align}$
$\begin{align}
  & \Rightarrow y=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}x-\dfrac{2at_{1}^{2}-2a{{t}_{1}}{{t}_{2}}-2at_{1}^{2}}{{{t}_{2}}+{{t}_{1}}} \\
 & \Rightarrow y=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}x+\dfrac{2a{{t}_{1}}{{t}_{2}}}{{{t}_{2}}+{{t}_{1}}} \\
\end{align}$
Let us substitute the value of ${{t}_{1}}{{t}_{2}}=-4$ in the above equation.
$\begin{align}
  & \Rightarrow y=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}x+\dfrac{2a{{t}_{1}}{{t}_{2}}}{{{t}_{2}}+{{t}_{1}}} \\
 & \Rightarrow y=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}x+\dfrac{2a\left( -4 \right)}{{{t}_{2}}+{{t}_{1}}} \\
 & \Rightarrow y=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}x-\dfrac{8a}{{{t}_{2}}+{{t}_{1}}} \\
\end{align}$
As we are given that the equation of the chord is $y=mx+c$, let us compare the both equations.
$\begin{align}
  & \Rightarrow m=\dfrac{2}{{{t}_{2}}+{{t}_{1}}} \\
 & \Rightarrow c=-\dfrac{8a}{{{t}_{2}}+{{t}_{1}}} \\
\end{align}$
As we need to find the value of c,
$\begin{align}
  & \Rightarrow c=-4a\left( \dfrac{2}{{{t}_{2}}+{{t}_{1}}} \right) \\
 & \Rightarrow c=-4am \\
\end{align}$
Hence the value of c is -4am.
Hence, the answer is Option A.

Note:
The general mistake one does while solving this problem is one might take the formula for perpendicular lines wrong as, when two lines with slopes ${{m}_{1}}$ and ${{m}_{2}}$are perpendicular then ${{m}_{1}}{{m}_{2}}=1$. But actually, it is ${{m}_{1}}{{m}_{2}}=-1$.