Question

If the bisector of the vertical angle of a triangle bisects the base, show that the triangle is isosceles.

Answer 1

Hint: First of all draw a triangle ABC and draw the bisector of \[\angle A\] which meets BC at D such that BD = DC. Now, extend AD to E such that AD = DE and prove \[\angle BAD\text{ }=\angle DEC\] by the congruence of triangles. Now, prove that AB = AC by using the sides opposite to equal angles are equal.

Complete step-by-step answer:
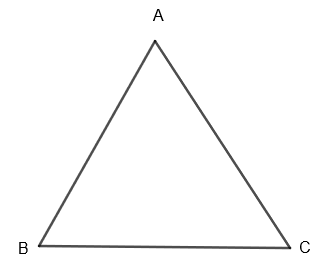
In this question, we are given that if the bisector of the vertical angle of a triangle bisects the base, we have to show that the triangle is isosceles. First of all, let us consider a triangle ABC.

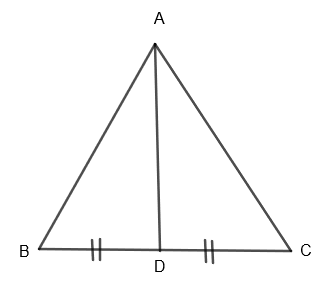
Let us draw AD which is the bisector of \[\angle A\] and meets at the base BC at D such that BD = DC and \[\angle BAD=\angle DAC\].

Now, extend AD to meet E such that AD = ED.

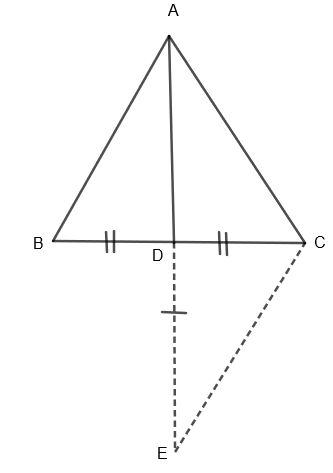
Now, let us consider \[\Delta ABD\] and \[\Delta ECD\] of the above figure. We are given that BD = DC. By construction, we have got AD = DE. Also, we know that vertically opposite angles at the intersection of the two lines are always equal. So, we get,
\[\angle ADB=\angle EDC\]
Hence, we get that \[\Delta ABD\] is congruent to \[\Delta ECD\] by side – angle – side (SAS) congruence criteria. We know that the corresponding sides of the congruent triangles are equal. So, we get,
\[AB=EC....\left( i \right)\]
Also, we know that the corresponding angles of the congruent triangles are equal. So, we get,
\[\angle BAD=\angle DEC.....\left( ii \right)\]
We are given that,
\[\angle BAD=\angle DAC.....\left( iii \right)\]
So, in \[\Delta ACE\], we get,
\[\angle AEC=\angle EAC\]
We know that in a triangle, sides opposite to equal angles are equal. So, we get,
\[EC=AC....\left( iv \right)\]
So, from equation (i) and (iv), we get,
AB = AC
We know that in an isosceles triangle, at least two sides are equal and we have got AB = AC. Hence \[\Delta ABC\] is an isosceles triangle.


Note: Students often make mistakes while writing corresponding parts of the congruent triangles. That is sometimes they may write BD = DE which is wrong. So, they must properly examine and then only write to get the correct answer. Also, students must remember that angles opposite to equal sides are equal and its converse is also true. Students should always draw the diagram first to visualize the question and always do the construction in further steps.