Question

If the area of the equilateral triangle inscribed inside the circle $ {{x}^{2}}+{{y}^{2}}+10x+12y+c=0 $ is $ 27\sqrt{3}sq. $ units, the value of c is:
a). 20
b). 25
c). 13
d). -25

Answer 1

Hint:
 We will use the concept of circle properties to solve the above question. We know that for general equation of the circle $ {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 $ , radius is equal to $ \sqrt{{{g}^{2}}+{{f}^{2}}-c} $ . Also, when an equilateral triangle is inscribed inside a circle, then each edge of the equilateral triangle makes an angle of $ 120{}^\circ $ at the centre of the circle. We will also use the property that when the perpendicular line is drawn from the centre of circle to the edge of the triangle then it also bisects the side of the triangle.

Complete step by step answer:
We can see from the question that we are given an equilateral triangle which is inscribed inside the circle. So, we will use the properties of the circle to solve the above question.
Let us say that C is the circle whose equation is given as: $ C={{x}^{2}}+{{y}^{2}}+10x+12y+c=0 $ , with centre O and let us assume that ABC is the equilateral triangle whose area is equal to $ 27\sqrt{3}sq. $ units.

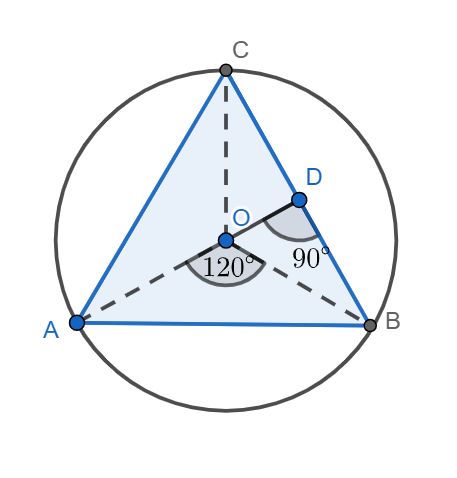
We can see from the figure that the line OA, OB, and OC divides the equilateral triangle ABC into three equal parts. So, from the properties of the equilateral triangle we know that line joining the centre of the circle to the vertex makes an angle of $ 120{}^\circ $ at the centre of the circle.
We also know that OA. OB and OC are the radius of the circle so they are equal and so we can say that triangles $ \Delta OAB,\Delta OBC,\Delta OAC $, are all isosceles triangles.
Now, from the properties of the isosceles triangle, we know that when we draw a perpendicular from vertex to the edge then it bisects the corresponding edge into two equal halves.
So, we can say that perpendicular OD drawn from centre to BC bisect the line BC.
Let us assume that ‘r’ is the radius of the circle.
So, in $ \Delta OBC $ , we know that $ \angle BOC=120{}^\circ $ , and $ \angle OBC=\angle OCB $ , because $ \Delta OBC $ is an isosceles triangle.
Thus, we can say that $ \angle OBC=\angle OCB=30{}^\circ $ .
Now, in the right triangle $ \Delta OBD $ , we can say that:
So, length of side OD = $ OB\sin 30{}^\circ $ = $ r\sin 30{}^\circ $ , as OB = r
Also, length of side BD = $ OB\cos 30{}^\circ $ = $ r\cos 30{}^\circ $
Since, we know that OD bisects line BC, so the length of line BC = Twice the length of line BD.
 $ \therefore BC=2BD=2r\cos 30{}^\circ $
Now, area of triangle $ \Delta OBD $ = $ \dfrac{1}{2}\times BC\times OD $
 $ =\dfrac{1}{2}\times 2r\cos 30{}^\circ \times r\sin 30{}^\circ $
 $ ={{r}^{2}}\times \dfrac{\sqrt{3}}{2}\times \dfrac{1}{2} $
 $ =\dfrac{\sqrt{3}}{4}{{r}^{2}} $
Since, we know that all the three triangles $ \Delta OAB,\Delta OBC,\Delta OAC $ has equal area.
So, area of $ \Delta ABC $ = $ 3\times \text{area of }\Delta OBC $
We know from question that area of $ \Delta ABC $ = $ 27\sqrt{3}sq. $ units.
 $ \Rightarrow 27\sqrt{3}=3\times \dfrac{\sqrt{3}}{4}{{r}^{2}} $
 $ \Rightarrow {{r}^{2}}=9\times 4 $
 $ \therefore r=6----\left( 1 \right) $
Now, we know that for general equation of the circle $ {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 $ , radius is equal to $ \sqrt{{{g}^{2}}+{{f}^{2}}-c} $ .
So, radius of circle whose equation is $ C={{x}^{2}}+{{y}^{2}}+10x+12y+c=0 $ = $ \sqrt{{{5}^{2}}+{{6}^{2}}-c} $ , because here g = 5 and f = 6.
Since, we have assumed that radius of the circle is ‘r’, so $ r=\sqrt{{{5}^{2}}+{{6}^{2}}-c} $
And, from (1) we know that r = 6. Thus, we can write:
 $ r=\sqrt{{{5}^{2}}+{{6}^{2}}-c}=6 $
 $ \Rightarrow 25+36-c={{6}^{2}} $
 $ \Rightarrow 25+36-36=c $
 $ \therefore c=25 $
Hence, option (b) is our required answer.

Note:
 Students are required to memorize the properties of the circle and also the properties of the triangle as they are applied here. We can also find the area of the equilateral triangle inscribed inside a circle whose radius is ‘r’ directly by using the formula $ 3\times \dfrac{1}{2}\times {{r}^{2}}\times \sin 120{}^\circ $ .