Question

If the arcs of same length in two circles subtends angles \[{{60}^{\circ }}\]and \[{{75}^{\circ }}\]at the centre, find the ratio of their radii.

Answer 1

Hint: When a certain external force is applied on a pendulum, it moves back and forth with periodic motion. So it is displaced by a certain angle and it is found using the formula \[l=r\theta \]here l is arc length and “r” is radius or length of pendulum. Convert the given degrees to radians and find the values for \[{{r}_{1}}\]and \[{{r}_{2}}\].

Complete step-by-step answer:

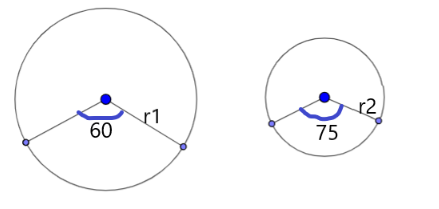
Given, the arcs of same length in two circles subtend \[{{60}^{\circ }}\]and \[{{75}^{\circ }}\]at the centre
Let the radii of two circles be \[{{r}_{1}}\]and \[{{r}_{2}}\]. Let an arc of length l subtends an angle \[{{60}^{\circ }}\]at the centre of circle of radius \[{{r}_{1}}\]
Now an arc of length l subtends an angle \[{{75}^{\circ }}\]at the centre of the circle of radius \[{{r}_{2}}\].
We know that the length of the arc is given by the formula \[l=r\theta \]
\[{{60}^{\circ }}=\dfrac{\pi }{3}radian\]and \[{{75}^{\circ }}=\dfrac{5\pi }{12}radian\]
\[l=\dfrac{{{r}_{1}}\pi }{3}\]for circle with radius \[{{r}_{1}}\]and arc length l . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1)
\[l=\dfrac{{{r}_{2}}5\pi }{12}\]for circle with radius \[{{r}_{2}}\]and arc length l . . . . . . . . . . . . . . . . . . . . . . . . . . (2)
Equation (1)=equation(2)
\[\dfrac{{{r}_{1}}\pi }{3}=\dfrac{{{r}_{2}}5\pi }{12}\]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)
\[\Rightarrow {{r}_{1}}=\dfrac{{{r}_{2}}5}{4}\]
\[\Rightarrow \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{5}{4}\]

Note: The length of the arc is given by formula \[l=r\theta \] in this \[\theta \] is the angle subtended and it is in radians but in the problem \[\theta \] is given in degrees so we have to convert to radians. To convert degrees to radians we have to multiply the given degrees with \[\dfrac{\pi }{180}\] then we will get angle subtended in radians.