Question

If the angle of incident is ${50^o}$, then calculate the angle between the incident ray and the reflected ray.
A. ${50^o}$
B. ${260^o}$
C. ${100^o}$
D. ${80^o}$

Answer 1

Hint: In this question, we need to determine the angle between the incident ray and the reflected ray. A normal line divides the angle between the incident ray and the reflected ray. These are divided into two equal angles. This implies that both the angles formed are equal.

Complete step by step answer:
According to the law of reflection,the angle of incidence is equal to the angle of reflection.the given example, the angle of incidence is ${50^o}$.Therefore, the angle of reflection will also be ${50^o}$.We can write this as,
The angle of incidence $ = $ the angle of reflection $ = $ ${50^o}$.

Now, we need to find out the angle between the incident ray and the reflected ray.Let \[\theta \] be the angle between the incident ray and the reflected ray.By observing the figure below, we can conclude that the sum of the angle of incidence and the angle of reflection equal to the measure of the angle between the incident ray and the reflected ray.

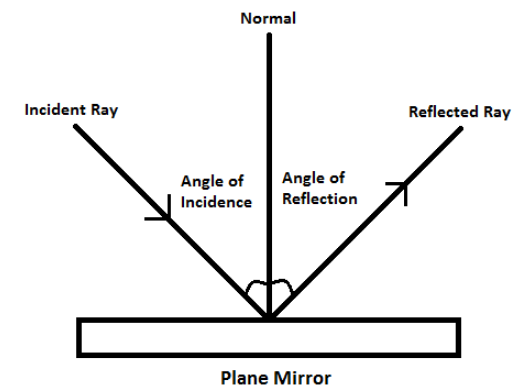
The angle between the incident ray and the reflected ray $ = $ the angle of incidence $ + $ the angle of reflection.
$
\theta = {50^o} + {50^o} \\
\therefore\theta = {100^o} $
Therefore, the angle between the incident ray and the reflected ray is ${100^o}$.

So, option C is the correct answer.

Note:Students get confused instead of calculating the angle between the incident ray and the reflected ray, they calculate the answer for the angle between the reflected ray and the normal. The angle between normal and the incident ray is called the angle of incidence. Similarly, the angle between the normal and the reflected ray is called the angle of reflection.