Question

If the angle of elevation of the cloud from a point h meter above a lake has a measure \[\alpha \] and the angle of depression of its reflection of the lake has a measure \[\beta \] .
Prove that the height of the cloud is \[\dfrac{h\left( \tan \beta +\tan \alpha \right)}{\left( \tan \beta -\tan \alpha \right)}\] .

Answer 1

Hint: We will find the values of \[\tan \alpha \] and \[\tan \beta \] as ratios of sides of the triangle. Then we will solve the two equations to get a combined equation which would be our final answer.

Complete step-by-step answer:

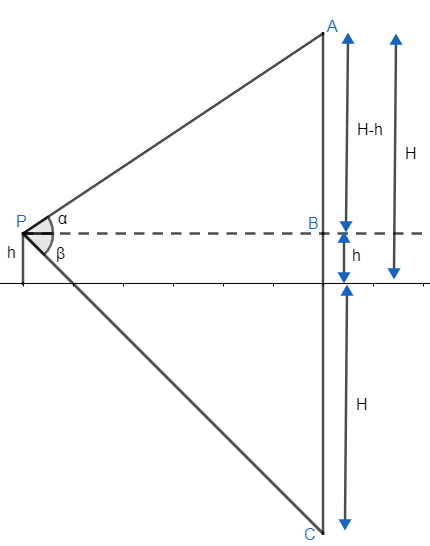
Now as we can see in the figure, let us assume that the point P is h above the lake.
Now let the cloud be at point A at a height of H. Let the line PB be the line of sight.
Also the reflection is at a depth of H below the lake since the height of the object and the depth of its reflection is equal.
Therefore, AB = H-h and BC = H+h.
Thus the angle \[\angle APB=\alpha \] .
Thus \[\tan \alpha =\dfrac{H-h}{PB}..........\left( i \right)\] .
Now, \[\angle BPC=\beta \] .
Therefore, \[\tan \beta =\dfrac{H+h}{PB}..........\left( ii \right)\]
Now dividing (i) by (ii) we get,
\[\dfrac{\tan \alpha }{\tan \beta }=\dfrac{\dfrac{H-h}{PB}}{\dfrac{H+h}{PB}}\]
Cancelling the common term PB, we get,
\[\dfrac{\tan \alpha }{\tan \beta }=\dfrac{H-h}{H+h}\]
Now cross multiplying we get,
\[\begin{align}
& \left( H+h \right)\tan \alpha =\left( H-h \right)\tan \beta \\
& H\tan \alpha +h\tan \alpha =H\tan \beta -h\tan \beta \\
\end{align}\]
Taking all the H terms on one side and all the h terms on the other we get,
\[\begin{align}
& H\tan \alpha -H\tan \beta =h\tan \alpha +h\tan \beta \\
& H\left( \tan \alpha -\tan \beta \right)=h\left( \tan \alpha +\tan \beta \right) \\
\end{align}\]
Cross multiplying we get,
\[H=\dfrac{h\left( \tan \alpha +\tan \beta \right)}{\left( \tan \alpha -\tan \beta \right)}\] .
Thus proved.
Note: Please remember that the height of the object and depth of its reflection is always equal from the ground point and not from the line of sight. You can commit a mistake there by taking the height and depth to be equal from the line of sight and mess up with the solution.