Question

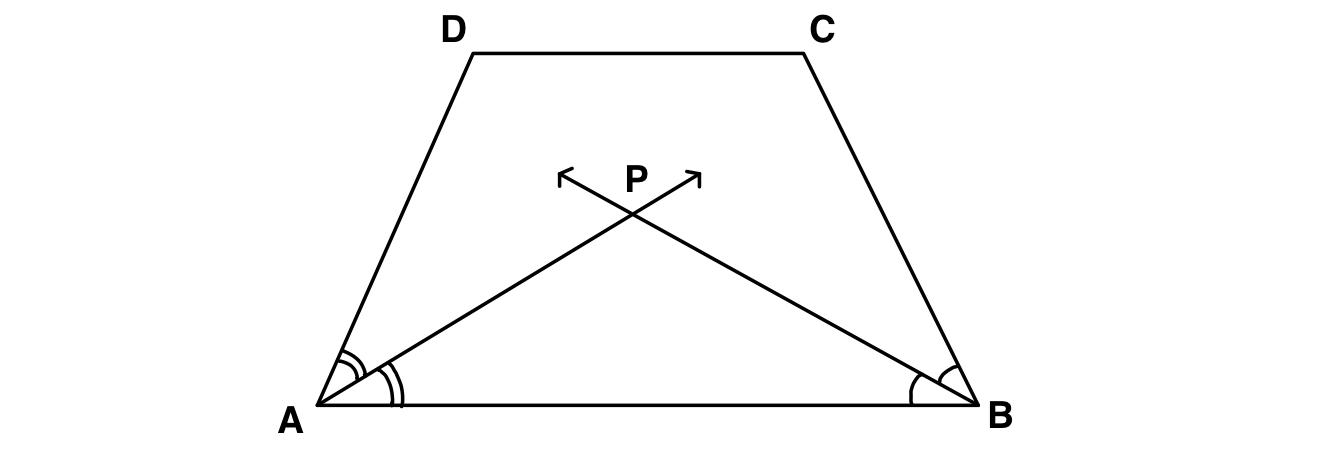
If the angle bisectors of $$\angle DAB$$ and $$\angle CAB$$ of any quadrilateral $$\square ABCD$$ intersects at the point P, then find $$2\ m\angle APB$$:(Given AB and CD are parallel)

A. $$\angle C+\angle D$$
B. $$\angle C+\angle B$$
C. $$\angle A+\angle B$$
D. $$\angle A+\angle D$$

Answer 1

Hint: In this question it is given that the angle bisectors of $$\angle DAB$$ and $$\angle CAB$$ of any quadrilateral $$\square ABCD$$ intersects at the point P, we have to find the value of $$2\ m\angle APB$$ where $$m\angle APB$$ is measure of $$\angle APB$$. So to find the solution we need to know that the summation of all angles of a triangle is $$180^{\circ}$$ and by using this formula in $$\triangle APB$$ we will get our required solution.

Complete step-by-step answer:
Here it is given that the angle bisectors of $$\angle DAB$$ and $$\angle CAB$$ of any quadrilateral $$\square ABCD$$ intersect at the point P.
Which implies, AP and BP are the bisector of $$\angle DAB$$ and $$\angle CAB$$,
i.e, $$\angle DAP=\angle PAB$$, $$\angle CBP=\angle PBA$$
And also $$\angle PAB=\dfrac{1}{2} \angle A$$, $$\angle PBA=\dfrac{1}{2} \angle B$$
Now let us assume that
$$m\angle DAP=m\angle PAB=x$$ and $$m\angle CBP=m\angle PBA=y$$
Therefore, $$x=\dfrac{1}{2} \angle A$$ and $$y=\dfrac{1}{2} \angle B$$
Now for $$\triangle APB$$, as we know that the summation of the measures of all angles of a triangle is $$180^{\circ}$$, so we can write,
$$\angle APB+\angle PAB+\angle PBA=180^{\circ }$$
$$\Rightarrow \angle APB+x+y=180^{\circ }$$
$$\Rightarrow \angle APB=180^{\circ }-x-y$$
$$\Rightarrow \angle APB=180^{\circ }-\left( x+y\right) $$
$$\Rightarrow \angle APB=180^{\circ }-\left( \dfrac{1}{2} \angle A+\dfrac{1}{2} \angle B\right) $$
$$\Rightarrow \angle APB=180^{\circ }-\dfrac{1}{2} \left( \angle A+\angle B\right) $$..........(1)
Now as we know that summation of all angles of a quadrilateral is $$360^{\circ}$$, so for quadrilateral ABCD we can write,
$$\angle A+\angle B+\angle C+\angle D=360^{\circ }$$
$$\Rightarrow \angle A+\angle B=360^{\circ }-\angle C-\angle D$$.......(2)
Now by putting the value of $$\angle A+\angle B$$ in equation (1) we get,
$$\Rightarrow \angle APB=180^{\circ }-\dfrac{1}{2} \left( 360^{\circ }-\angle C-\angle D\right) $$
$$\Rightarrow \angle APB=180^{\circ }-\dfrac{360^{\circ }}{2}+\dfrac{1}{2} \angle C+\dfrac{1}{2} \angle D$$
$$\Rightarrow \angle APB=180^{\circ }-180^{\circ }+\dfrac{1}{2} (\angle C+\angle D)$$
$$\Rightarrow \angle APB=\dfrac{1}{2} (\angle C+\angle D)$$
Therefore we can write
Measure of $$\angle APB=\dfrac{1}{2} (\angle C+\angle D)$$
i.e, $$ m\angle APB=\dfrac{1}{2} (\angle C+\angle D)$$
Which implies, $$\Rightarrow 2\times m\angle APB=\angle C+\angle D$$
Which is our required solution.
Hence the correct option is option A.

Note: While solving this type of question you need to know that when a straight line bisects an angle then it divides that angle into two equal parts or we can say that the measures of new two angles is equal and also for any quadrilateral the summation of the measures of its all angles is $$360^{\circ}$$.