Question

If the angle between the tangents drawn from an external point P to a circle of radius a and centre O, is $60{}^\circ $ , find the length of OP.

Answer 1

Hint: Start by drawing a representative diagram of the above situation and mark the points of intersection of the tangents with the circle as A and E. Now use the property that the tangents from a given point to the circle have equal lengths and the angle between them is bisected by the line joining the point to the centre of the circle. Finally use simple trigonometric ratios to find the length of OP.

Complete step-by-step answer:
Let us start by drawing a representative diagram of the situation mentioned in the question.

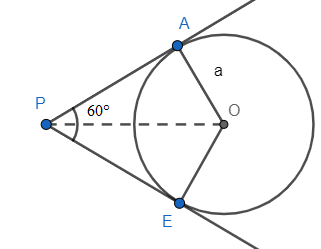
In the above figure, AP and EP are the tangents to the circle with centre O and radius a. Now we know that the tangents from a given point to the circle have equal lengths and the angle between them is bisected by the line joining the point to the centre of the circle. So, we can say that:
$\angle APO=\dfrac{1}{2}\times 60{}^\circ =30{}^\circ $ .
Now, if we see in $\Delta APO$ , angle OAP is $90{}^\circ $ as the angle between radius and tangent of a circle is always $90{}^\circ $ . Also, $\angle APO=30{}^\circ $ and AO is the radius, so AO=a. As it is a right angled triangle, we will use trigonometry to find the length of OP.
We know $\sin x=\dfrac{perpendicular}{hypotenuse.}$
In our triangle, for $x=\angle APO$ , AO is the perpendicular and OP is the hypotenuse.
$\therefore \sin \left( \angle APO \right)=\dfrac{AO}{OP}$
$\Rightarrow \sin 30{}^\circ =\dfrac{a}{OP}$
Now we know that the value of $\sin 30{}^\circ =\dfrac{1}{2}$ . So, our equation becomes:
$\dfrac{1}{2}=\dfrac{a}{OP}$
On cross-multiplication, we get
$OP=2a$
Therefore, the length of OP is 2a units.

Note: If you want, you can directly use the property that length of a tangent to a circle from a given point is equal to $\sqrt{{{S}_{1}}}$ , where ${{S}_{1}}$ is the value you get by putting the point from which tangent is drawn in the equation of the circle. Also, be careful and must use the unit with your answer while reporting the answer. It is also prescribed that you learn the values of trigonometric ratios for all standard angles, as they are used very often.