Question

If tangents TA and TB from a point T to a circle with center O are inclined to each other at an angle of \[{{70}^{\circ }}\], then find \[\angle AOB\] (in degrees).

Answer 1

Hint: Draw the figure as mentioned. The tangents and normal are at a point on a circle as perpendicular to each other. Apply angle sum property of quadrilaterals and get \[\angle AOB\].

Complete step-by-step answer:

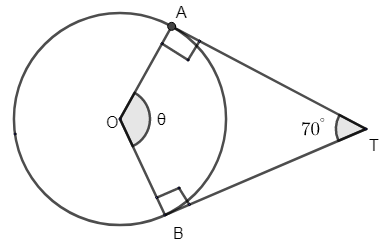
From the figure you can find a circle with center O. Let T be the point where the tangent starts. Thus TA and TB are tangents from the point T to the point A and B of the circle respectively.
It is said that they are inclined at an angle of \[{{70}^{\circ }}\]. Thus from the figure we can say that, \[\angle ATB={{70}^{\circ }}\].
The tangent to a circle is a line that touches the circle at one point, to the circle is always perpendicular to the radius.
Thus we can say that tangents and normal at a point on a circle are perpendicular to the radius.
Thus we can say that tangents and normal at a point on a circle are perpendicular to each other. Thus we can say that the circles are perpendicular to each other. Thus we can say that, \[\angle A={{90}^{\circ }}\] and \[\angle B={{90}^{\circ }}\] [from the figure].
We know that in a quadrilateral, the sum of all angles is \[{{360}^{\circ }}\].
Similarly by looking in the figure, we can say that,
\[\angle A+\angle B+\angle O+\angle T={{360}^{\circ }}\]
We know, \[\angle A={{90}^{\circ }}\], \[\angle B={{90}^{\circ }}\] and \[\angle T={{70}^{\circ }}\]. Thus substitute these values and get \[\angle O\].
\[\begin{align}
  & \angle A+\angle B+\angle O+\angle T={{360}^{\circ }} \\
 & {{90}^{\circ }}+{{90}^{\circ }}+\angle O+{{90}^{\circ }}={{360}^{\circ }} \\
 & \angle O={{360}^{\circ }}-{{90}^{\circ }}-{{90}^{\circ }}-{{70}^{\circ }} \\
 & \angle O={{360}^{\circ }}-{{180}^{\circ }}-{{70}^{\circ }} \\
 & \angle O={{360}^{\circ }}-{{250}^{\circ }} \\
 & \angle O={{110}^{\circ }} \\
\end{align}\]
Thus we got, \[\angle AOB={{110}^{\circ }}\].
\[\therefore \] We got the required angle AOB as \[{{110}^{\circ }}\] (in degrees).

Note: We know the angle sum property of a quadrilateral corresponds to \[{{360}^{\circ }}\]. You may sometimes take it as \[{{180}^{\circ }}\], which is the total angle sum in a triangle. Don’t mix between the angle’s sum of triangles and quadrilaterals.