Question

If $\tan \theta =\dfrac{3}{4}$ find the sine, cosine, versine and cosecant of $\theta $.

Answer 1

Hint: Here, we are going to apply the trigonometric ratio formula in the above question. There are fundamentally six major trigonometric functions, i.e. sine, cosine, tangent, cotangent, cosecant, secant. Here, in this question we have a term 'versine'. Versine means versed sine. It is a trigonometric function already appearing in some of the earliest trigonometric tables. It is written as versin$\left( \theta \right)$. So, here the approach will be: make one right angled triangle and with the help of given condition find all the dimensions of the right angle triangle which can be used further for finding other required trigonometric functions.

Complete step by step answer:
Now, let’s move to the solution part:
We have been given data as $\tan \theta =\dfrac{3}{4}$ and we have to find
$\sin \theta =?,\cos \theta =?,\text{versin}\left( \theta \right)=?,\text{cosec}\left( \theta \right)=?$

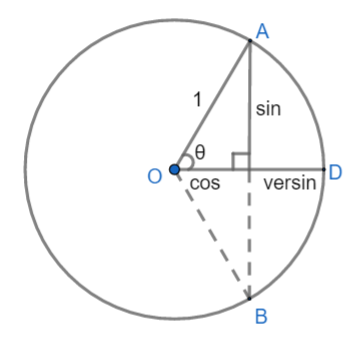
Sine, cosine and versine of angle $\theta $ in terms of unit circle with radius 1, centered at O.
Versine can be expressed as:
\[\text{versine}\left( \theta \right)=1-\cos \left( \theta \right)=2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)\]
Now, we have $\tan \theta =\dfrac{3}{4}$.
Let us make a right angled triangle ABC, i.e.

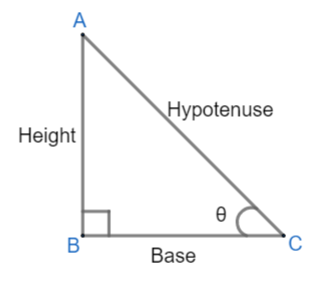
Here, $\angle ACB=\theta $,
AB = height or perpendicular
BC = base
AC = hypotenuse
Now, we know,
\[\begin{align}
  & \tan \theta =\dfrac{\text{Height}}{\text{Base}}=\dfrac{AB}{BC} \\
 & \sin \theta =\dfrac{\text{Height}}{\text{Hypotenuse}}=\dfrac{AB}{AC} \\
 & \cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}=\dfrac{BC}{AC} \\
 & \text{cosec}\theta =\dfrac{1}{\sin \theta }\Rightarrow \text{cosec}\theta =\dfrac{AC}{AB} \\
\end{align}\]
Now according to property right angle triangle, we know,
\[\begin{align}
  & {{\left( \text{Base} \right)}^{2}}+{{\left( \text{Perpendicular} \right)}^{2}}={{\left( \text{Hypotenuse} \right)}^{2}} \\
 & {{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}={{\left( AC \right)}^{2}} \\
\end{align}\]
Now, $\tan \theta =\dfrac{3}{4}=\dfrac{AB}{BC}$.
So, here we can take, AB = 3x and BC = 4x.
Now, \[{{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}={{\left( AC \right)}^{2}}\]
So by putting the value of AB and BC we get:
\[\begin{align}
  & {{\left( 4x \right)}^{2}}+{{\left( 3x \right)}^{2}}={{\left( AC \right)}^{2}} \\
 & \Rightarrow {{\left( AC \right)}^{2}}=25{{x}^{2}} \\
 & \Rightarrow AC=\sqrt{25{{x}^{2}}} \\
 & \Rightarrow AC=\pm 5x \\
\end{align}\]
But the side can't be negative, AC = +5x.
Now, we know, $\sin \theta =\dfrac{AB}{AC}$.
Therefore, by putting value of AB and AC, we get:
\[\sin \theta =\dfrac{3x}{5x}=\dfrac{3}{5}\]
Similarly,
\[\begin{align}
  & \cos \theta =\dfrac{BC}{AC} \\
 & \cos \theta =\dfrac{4x}{5x}=\dfrac{4}{5} \\
\end{align}\]
We have already stated the formula for versine $\left( \theta \right)$ i.e.
\[\Rightarrow \text{versine}\left( \theta \right)=1-\cos \theta =1-\dfrac{4}{5}=\dfrac{1}{5}\]
Now, we know $\text{cosec}\theta =\dfrac{1}{\sin \theta }$.
We have already calculated the value of $\sin \theta =\dfrac{3}{5}$.
\[\therefore \text{cosec}\theta =\dfrac{1}{\dfrac{3}{5}}=\left( \dfrac{5}{3} \right)\]

Note: Students sometimes get confused with the sides nomenclature in the right angled triangle i.e. how to decide which side should be considered as height (or perpendicular) and which side should be considered as base. So, the answer is the side which is just in front of angle $\theta $ or the side opposite to the angle $\theta $ will be always considered as perpendicular (or height) and the side which is in front or opposite to the right angle will always be the hypotenuse and then remaining side will automatically considered as base.
We can also use some basic identities for finding the remaining trigonometric functions, if 2-3 basic trigonometric ratio are given:
\[\begin{align}
  & *{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\
 & *1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta \\
 & *1+{{\cot }^{2}}\theta =\text{cose}{{\text{c}}^{2}}\theta \\
\end{align}\]