Question

If \[\tan 2A=\cot \left( A-{{18}^{o}} \right)\]where \[2A\] is an acute angle, find the
 value of\[A\].

Answer 1

Hint: Relate \[\tan \theta \]and \[\cot \theta \] by changing their angles
 (complementary to each other).
Here, we have given condition for calculation of angle \[A\] is
\[\tan 2A=\cot \left( A-{{18}^{o}} \right).....\left( i \right)\]
As we know that \[\tan \theta \]and \[\cot \theta \], both are reciprocal functions and can be
 related in the following way: \[\tan \left( 90-\theta \right)=\cot \theta .....\left( ii \right)\]
Now, we can use property \[\left( ii \right)\]with the equation \[\left( i \right)\] to replace
 \[\cot \left( A-{{18}^{o}} \right)\]
Let, \[A-{{18}^{o}}=\theta .....\left( iii \right)\]
So, the equation \[\left( i \right)\]becomes
\[\tan 2A=\cot \theta \]
Now, by using the equation \[\left( i \right)\], we can put \[\cot \theta =\tan \left( 90-\theta
  \right)\] in the following manner:
\[\tan 2A=\cot \theta \]
\[\tan 2A=\tan \left( 90-\theta \right).....\left( iv \right)\]
As we know that if \[\tan {{\theta }_{1}}=\tan {{\theta }_{2}}\], then \[{{\theta }_{1}}\] and
 \[{{\theta }_{2}}\] must be equal to get the same tangent of angles.
Hence, from the equation \[\left( iv \right)\], we can write
\[2A=90-\theta \]
Now, we already have \[\theta =A-18\] from the equation \[\left( iii \right)\].
Therefore, \[2A=90-\left( A-18 \right)\]
\[2A=90-A+18\]
\[3A=108\]
\[A={{36}^{o}}\]
As we already have given that \[A\] is an acute angle, so \[A={{36}^{o}}\] is correct.
Now, from \[\tan {{\theta }_{1}}=\tan {{\theta }_{2}}\], we can get infinite solutions by writing
 the general solution of it in the following way:
If \[\tan {{\theta }_{1}}=\tan {{\theta }_{2}}\]
\[{{\theta }_{1}}=n\pi +{{\theta }_{2}}\] where \[n\in Z\left( n=0,1,2,3.... \right)\]
Hence, we can calculate more numbers of angles \[A\] but we need only an acute angle as
 mentioned in the question. So, we need to find only the principle solution of \[\tan {{\theta
 }_{1}}=\tan {{\theta }_{2}}\]or
\[\tan 2A=\tan \left( 108-A \right)\]
\[2A=n\pi +108-A\]
\[3A=n\pi +108\]
\[A=\dfrac{n\pi }{3}+36\]; \[n=0,1,2,3....\]
For, \[n=0,A={{36}^{o}}\] and for any other \[n\], \[A\] will be more than \[{{90}^{o}}\]. Hence
 that will not be the correct solution for the given question.

Note: We can calculate angle \[A\] by converting \[\tan 2A\]to \[\cot \] function by using
 \[\tan \theta =\cot \left( 90-\theta \right)\]
We have \[\tan 2A=\cot \left( A-18 \right)\]
\[\cot \left( 90-2A \right)=\cot \left( A-18 \right)\]
\[90-2A=A-18\]
\[A={{36}^{o}}\]
We can make a mistake when writing the equation \[\tan \left( 90-\theta \right)=\cot \theta
 \]. One can get confused in the conversion of one function to another. So, he/she must use
 the quadrant rules as follows.

(1)
 

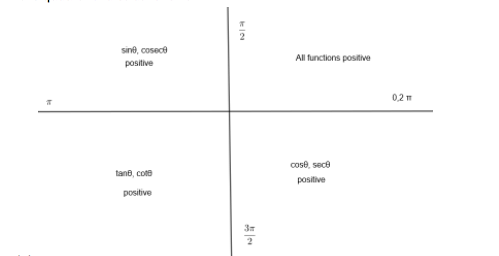
(2) If the conversion is done like \[\dfrac{n\pi }{2}+\theta \] type, then we need to change
\[\tan \theta \rightleftarrows \cot \theta \]
\[\sin \theta \rightleftarrows \cos \theta \]
\[\text{cosec}\theta \rightleftarrows \sec \theta \]
where \[n\] is an odd integer.
If the conversion is like \[\left( n\pi +\theta \right)\] type, then we need not convert any
 function to others only taking care of signs should be involved.
Example:
(1) \[\sin \left( \dfrac{\pi }{2}+\theta \right)=\cos \theta \]
\[\dfrac{\pi }{2}+\theta \]will lie in the second quadrant, so \[\sin \] will be positive.
(2) \[\sin \left( \dfrac{3\pi }{2}+\theta \right)=-\cos \theta \]
\[\dfrac{3\pi }{2}+\theta \]will lie in the \[{{4}^{th}}\] quadrant.
(3) \[\tan \left( 2\pi -\theta \right)=-\tan \theta \]
\[2\pi -\theta \]will lie in the \[{{4}^{th}}\] quadrant.