Question

If $\sec \theta =x+\dfrac{1}{4x}$, then the value of $\sec \theta +\tan \theta $ is
[a] 2x
[b] $\dfrac{1}{2x}$
[c] 4x
[d] None of these.

Answer 1

Hint: Use the trigonometric identity ${{\sec }^{2}}\theta -1={{\tan }^{2}}\theta $and hence find the value of $\tan \theta $ and hence find the value of $\sec \theta +\tan \theta $. Alternatively, write $\sec \theta $ and $\tan \theta $ as the ratios of sides of a triangle. Think what the sides of the triangle could be to satisfy the equation for $\sec \theta $ and hence find the value of $\tan \theta $ and hence the value of $\sec \theta +\tan \theta $.

Complete step-by-step answer:
Trigonometric ratios:
There are six trigonometric ratios defined on an angle of a right-angled triangle, viz sine, cosine,
tangent, cotangent, secant and cosecant.
The sine of an angle is defined as the ratio of the opposite side to the hypotenuse.
The cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse.
The tangent of an angle is defined as the ratio of the opposite side to the adjacent side.
The cotangent of an angle is defined as the ratio of the adjacent side to the opposite side.
The secant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
The cosecant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
Observe that sine and cosecant are multiplicative inverses of each other, cosine and secant are
multiplicative inverses of each other, and tangent and cotangent are multiplicative inverses of each
other.
We have ${{\sin }^{2}}x+{{\cos }^{2}}x=1,{{\sec }^{2}}x=1+{{\tan }^{2}}x$ and ${{\csc }^{2}}x=1+{{\cot }^{2}}x$. These identities are called Pythagorean identities.
Now, we have
$\sec \theta =x+\dfrac{1}{4x}=\dfrac{1+4{{x}^{2}}}{4x}$
Using ${{\sec }^{2}}\theta -1={{\tan }^{2}}\theta $, we get
$\begin{align}
  & {{\left( \dfrac{1+4{{x}^{2}}}{4x} \right)}^{2}}-1={{\tan }^{2}}\theta \\
 & \Rightarrow {{\tan }^{2}}\theta =\dfrac{1+16{{x}^{4}}+8{{x}^{2}}}{16{{x}^{2}}}-1 \\
 & \Rightarrow {{\tan }^{2}}\theta =\dfrac{1+16{{x}^{4}}-8{{x}^{2}}}{16{{x}^{2}}} \\
 & \Rightarrow {{\tan }^{2}}\theta ={{\left( \dfrac{4{{x}^{2}}-1}{4x} \right)}^{2}} \\
 & \Rightarrow \tan \theta =x-\dfrac{1}{4x}\text{ or }-x+\dfrac{1}{4x} \\
\end{align}$
Hence
 \[\begin{align}
  & \sec \theta +\tan \theta =x+\dfrac{1}{4x}+x-\dfrac{1}{4x}\text{ or }x+\dfrac{1}{4x}-x+\dfrac{1}{4x} \\
 & \Rightarrow \sec \theta +\tan \theta =2x\text{ or }\dfrac{1}{2x} \\
\end{align}\]
Hence options [a] and [b] are correct.

Note: Alternative solution:

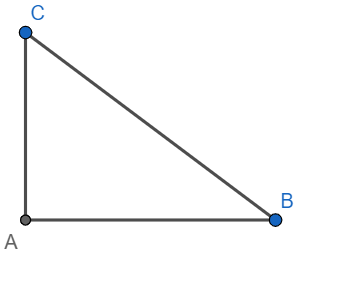
Let AB = 4x and BC $=4{{x}^{2}}+1$
Hence, AC = $\pm \sqrt{{{\left( 4{{x}^{2}}+1 \right)}^{2}}-{{\left( 4x \right)}^{2}}}=\pm \left( 4{{x}^{2}}-1 \right)$
Hence $\tan \theta =\dfrac{\pm \left( 4{{x}^{2}}-1 \right)}{4x}=-x+\dfrac{1}{4x}\text{ or }x-\dfrac{1}{4x}$
Hence $\sec \theta +\tan \theta =2x\text{ or }\dfrac{1}{2x}$.