Question

If \[{{S}_{1}}\text{ and }{{S}_{2}}\] are the foci of the hyperbola whose transverse axis length is 4 and conjugate axis length is 6. \[{{S}_{3}}\text{ and }{{S}_{4}}\] are the foci of the conjugate hyperbola, then the area of the quadrilateral \[{{S}_{1}}{{S}_{3}}{{S}_{2}}{{S}_{4}}\] is:
(a) 24
(b) 26
(c) 22
(d) None of these

Answer 1

Hint: In order to solve this question, we need to know that for any hyperbola, the length of the transverse axis is given by 2a, and the length of the conjugate axis is given by 2b and for the conjugate hyperbola these values interchange. Also, we need to remember that the coordinate of foci is given by (ae, 0) and (– ae, 0). So, foci of conjugate will be given by (0, be) and (0, – be). Also, the eccentricity of the hyperbola is given by \[e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}\] for general hyperbola.

Complete step-by-step answer:

In this question, we have been asked to find the area of the quadrilateral formed by the foci of the hyperbola and its conjugate when it is given that the length of the conjugate axis is 6 and transverse axis is 4. To solve this question, we will first draw the figure according to the given conditions.

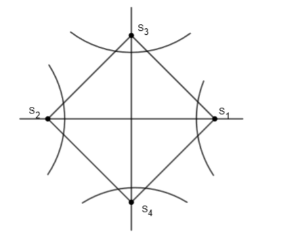
Here, we have represented the hyperbola with foci \[{{S}_{1}}\text{ and }{{S}_{2}}\] as general hyperbola of the equation \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] whose foci are \[{{S}_{1}}\left( a{{e}_{1}},0 \right)\text{ and }{{S}_{2}}\left( -a{{e}_{1}},0 \right)\] and the length of the conjugate axis is 2b, and the length of the transverse axis is 2a. And the eccentricity is given by \[{{e}_{2}}=\sqrt{1+\dfrac{{{a}^{2}}}{{{b}^{2}}}}\]
So, we can say,
2b = 6
b = 3
And 2a = 4
a = 2
Therefore, we can say eccentricity,
\[{{e}_{1}}=\sqrt{1+\dfrac{{{\left( 3 \right)}^{2}}}{{{2}^{2}}}}=\sqrt{1+\dfrac{9}{4}}=\dfrac{\sqrt{13}}{2}\]
Hence, we get the coordinates of the foci as \[{{S}_{1}}\left( 2\left( \dfrac{\sqrt{13}}{2} \right),0 \right)={{S}_{1}}\left( \sqrt{13},0 \right)\text{ and }{{S}_{2}}\left( -\sqrt{13},0 \right)\].
Also, from the figure, we have represented conjugate of hyperbola, having equation \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] with an equation \[\dfrac{{{y}^{2}}}{{{b}^{2}}}-\dfrac{{{x}^{2}}}{{{a}^{2}}}=1\] whose foci are given by \[{{S}_{3}}\left( 0,be \right)\text{ and }{{S}_{4}}\left( 0,-be \right)\]. And eccentricity is given by
\[{{e}_{2}}=\sqrt{1+\dfrac{{{a}^{2}}}{{{b}^{2}}}}\]
\[=\sqrt{1+\dfrac{{{\left( 2 \right)}^{2}}}{{{\left( 3 \right)}^{2}}}}\]
\[=\sqrt{1+\dfrac{4}{9}}\]
\[=\dfrac{\sqrt{13}}{3}\]
Hence, we can say foci \[{{S}_{3}}\text{ and }{{S}_{4}}\] are \[{{S}_{3}}\left( 0,3\times \dfrac{\sqrt{13}}{3} \right)\text{ and }{{S}_{4}}\left( 0,-3\times \dfrac{\sqrt{13}}{3} \right)\] that are \[{{S}_{3}}\left( 0,\sqrt{13} \right)\text{ and }{{S}_{4}}\left( 0,-\sqrt{13} \right)\]. Now, we know that the quadrilateral formed the foci of a hyperbola and its conjugate a square by comparing the coordinates of \[{{S}_{1}},{{S}_{2}},{{S}_{3}}\text{ and }{{S}_{4}}\]. So, we can say \[{{S}_{1}}{{S}_{3}}{{S}_{2}}{{S}_{4}}\] is a square. And, we know that the area of the square is given by the side \[\times \] side. So, we can write,
\[\text{Area of }{{S}_{1}}{{S}_{3}}{{S}_{2}}{{S}_{4}}={{\left( {{S}_{1}}{{S}_{3}} \right)}^{2}}\]
Now, we know the distance between two points \[\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)\] is given by \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]. So, we get,
\[\left( {{x}_{1}},{{y}_{1}} \right)={{S}_{1}}\left( \sqrt{13},0 \right)\]
\[\left( {{x}_{2}},{{y}_{2}} \right)={{S}_{3}}\left( 0,\sqrt{13} \right)\]
Therefore, we get,
\[{{S}_{1}}{{S}_{3}}=\sqrt{{{\left( 0-\sqrt{13} \right)}^{2}}+{{\left( \sqrt{13}-0 \right)}^{2}}}\]
\[{{S}_{1}}{{S}_{3}}=\sqrt{13+13}=\sqrt{26}\]
Hence, we can say that
\[\text{Area of }{{S}_{1}}{{S}_{3}}{{S}_{2}}{{S}_{4}}={{\left( \sqrt{26} \right)}^{2}}\]
= 26 sq. units
Hence, we can say that the area of the quadrilateral formed by the foci of the hyperbola and its conjugate is 26 sq. units.
Therefore, option (b) is the correct answer.

Note: This question can be quite confusing if we do not pay attention to. So, we have to be very focused also as we can make a lot of mistakes while writing the equation of the conjugate of the hyperbola of \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] which is \[\dfrac{{{y}^{2}}}{{{b}^{2}}}-\dfrac{{{x}^{2}}}{{{a}^{2}}}=1\]. Also, we need to remember that for hyperbola, \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\], eccentricity is given by \[e=\sqrt{1+\dfrac{{{b}^{2}}}{{{a}^{2}}}}\] and foci as (ae, 0) and (– ae, 0).