Question

If S is the circumcentre, O is the orthocentre of $\Delta ABC$, then $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=$
A. $\overrightarrow{SO}$
B. $2\overrightarrow{SO}$
C. $\overrightarrow{OS}$
D. $2\overrightarrow{OS}$

Answer 1

Hint: We here need to find the value of $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}$. To find this, we will construct the $\Delta ABC$ in which we will construct any two altitudes so that their point of intersection will give us its orthocentre as O. We will also construct its circumcircle so that we will get its circumcentre S. Through S, we will construct SP, SQ, and SR which will be the perpendicular bisectors to BC, AC and AB respectively. Then we will mark their directions such that we get the required vectors $\overrightarrow{AO}$ ,$\overrightarrow{SA},\overrightarrow{SB}$,$\overrightarrow{SC}$,$\overrightarrow{SP},\overrightarrow{SQ}$,$\overrightarrow{SR}$, $\overrightarrow{PB}$,$\overrightarrow{PC}$ and $\overrightarrow{SO}$. After that, we will try to find a relationship between $\overrightarrow{SP}$ and $\overrightarrow{AO}$ through geometry as they are parallel. Then from the property of vector addition we will be able to see that $\overrightarrow{SP}+\overrightarrow{PB}=\overrightarrow{SB}$ and $\overrightarrow{SP}+\overrightarrow{PC}=\overrightarrow{SC}$. After that, we will put all these values in $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}$ and solve the vectors. Hence, we will obtain an answer.

Complete step-by-step solution
Now, we know that the circumcentre of a triangle is the center of a circle formed by inscribing that circle and the orthocentre is the point of intersection of all the perpendiculars in a triangle.
Thus, in the $\Delta ABC$, let us construct any two perpendiculars and its circumcircle.
The point of intersection of the perpendiculars will give us the orthocentre O, and the center of the circumcircle will give us the circumcentre S.
Let the perpendiculars be AD and CE. This will give us the vectors $\overrightarrow{AD}$ and $\overrightarrow{CE}$. Since the orthocentre lies on this line, we will also get the vector $\overrightarrow{AO}$.
Let us also join SA, SB and SC so that the vectors $\overrightarrow{SA},\overrightarrow{SB}$ and $\overrightarrow{SC}$ are formed. After that, let us also join SO to form the vector $\overrightarrow{SO}$.
Now, let us construct SP, SQ, and SR which are the perpendicular bisectors of the chords BC, AC, and AB respectively. This will now give us the vectors $\overrightarrow{SP},\overrightarrow{SQ}$ and $\overrightarrow{SR}$. From this, we will also get vectors $\overrightarrow{PB}$ and $\overrightarrow{PC}$.
As a result, we get the vectors, $\overrightarrow{AO}$ ,$\overrightarrow{SA},\overrightarrow{SB}$,$\overrightarrow{SC}$,$\overrightarrow{SP},\overrightarrow{SQ}$,$\overrightarrow{SR}$, $\overrightarrow{PB}$,$\overrightarrow{PC}$ and $\overrightarrow{SO}$.

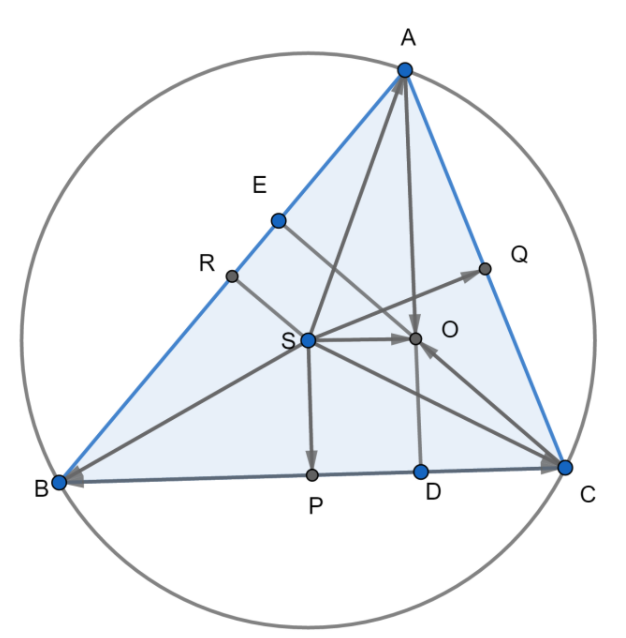
Now, we can see that SP||AO (because both these lines are perpendicular to the same line BC hence, we can say that BC is the transversal to SP and AO and their corresponding angles are equal as they are right angles).
Hence, we can say that $\overrightarrow{SP}||\overrightarrow{AO}$
Now, we know that when two vectors are parallel, one vector is $\lambda $ times the other vector where $\lambda $ is a real number.
Thus, we can say that:
$\overrightarrow{SP}=\lambda \overrightarrow{AO}$
Now, we know that the orthocentre divides the altitude in the ratio 2:1.
Thus, we can say that:
$\begin{align}
  & \dfrac{AO}{OD}=\dfrac{2}{1} \\
 & \Rightarrow AO=2OD \\
 & \Rightarrow OD=\dfrac{AO}{2} \\
\end{align}$
From the geometry of the figure, we can also see that OD=SP. Thus, we can conclude that:
$\begin{align}
  & OD=SP \\
 & \Rightarrow SP=\dfrac{AO}{2} \\
\end{align}$
Thus, in vector form, we can write it as:
$\overrightarrow{SP}=\dfrac{1}{2}\overrightarrow{AO}$
Thus, we can say that:
$\lambda =\dfrac{1}{2}$
Now, from the figure, we can also see that:
$\overrightarrow{SP}+\overrightarrow{PB}=\overrightarrow{SB}$ (property of vector addition)
Similarly, we can also see the same thing for $\overrightarrow{SC}$.
Hence, we can say that:
$\overrightarrow{SP}+\overrightarrow{PC}=\overrightarrow{SC}$
Now, we need to find the value of $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}$.
We can find this by putting the values of $\overrightarrow{SB}$ and $\overrightarrow{SC}$ in $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}$.
Thus, we can say that:
\[\begin{align}
  & \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+\overrightarrow{SP}+\overrightarrow{PB}+\overrightarrow{SP}+\overrightarrow{PC} \\
 & \Rightarrow \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+2\overrightarrow{SP}+\overrightarrow{PB}+\overrightarrow{PC} \\
\end{align}\]
Now, we have already established that $\overrightarrow{SP}=\dfrac{1}{2}\overrightarrow{AO}$.
Hence, putting this value in the obtained value of $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}$, we get:
\[\begin{align}
  & \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+2\overrightarrow{SP}+\overrightarrow{PB}+\overrightarrow{PC} \\
 & \Rightarrow \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+2\left( \dfrac{1}{2}\overrightarrow{AO} \right)+\overrightarrow{PB}+\overrightarrow{PC} \\
 & \Rightarrow \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+\overrightarrow{AO}+\overrightarrow{PB}+\overrightarrow{PC} \\
\end{align}\]
Now, we can see that $\overrightarrow{PB}$ and $\overrightarrow{PC}$ are opposite in direction and since we constructed SP as the perpendicular bisector of BC, P is the midpoint of BC and hence $\overrightarrow{PB}$ and $\overrightarrow{PC}$ will equal in magnitude.
Thus, we can say that:
$\overrightarrow{PB}=-\overrightarrow{PC}$
Thus, putting this value in the now obtained value of $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}$, we get:
\[\begin{align}
  & \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+\overrightarrow{AO}+\overrightarrow{PB}+\overrightarrow{PC} \\
 & \Rightarrow \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+\overrightarrow{AO}-\overrightarrow{PC}+\overrightarrow{PC} \\
 & \Rightarrow \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+\overrightarrow{AO} \\
\end{align}\]
Now, from the figure, we can also see that:
$\overrightarrow{SA}+\overrightarrow{AO}=\overrightarrow{SO}$ (property of vector addition)
Thus, putting this value in now obtained value of $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}$, we get:
$\begin{align}
  & \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SA}+\overrightarrow{AO} \\
 & \overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{SO} \\
\end{align}$
Hence, the value of $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}$ is $\overrightarrow{SO}$.
Thus, option (A) is the correct option.

Note: Be careful with the direction of vectors as even change in one of the directions of the vectors could result in a wrong answer as two vectors are only equal if both their direction and magnitude are equal and committing a mistake in giving the direction is highly likely. Also, in the question, we mentioned the property of vector addition. It is given as:
Let there be two vectors,$\vec{a}$ and $\vec{b}$making any angle with each other. Now, let us join these vectors such that $\vec{a}=\overrightarrow{AB}$ and $\vec{b}=\overrightarrow{BC}$.
This is shown as follows:

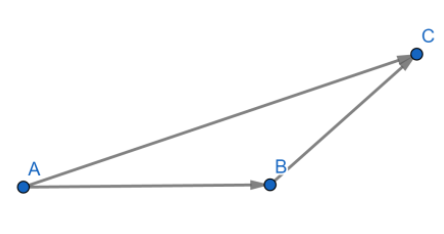
Here, the vector represented as $\overrightarrow{AC}$ will be their sum. Thus, we can write it as:
$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$