
If Q(0,1) is equidistant from P(5,-3) and R(x,6), find the values of x. Also find the distance QR and PR.
Answer
615.6k+ views
Hint: In this question it is given that the point Q(0,1) is equidistant from P(5,-3) and R(x,6), then we have to find the values of x. Also have to find QR and PR. So for this we have to know the distance formula between two points, which states that, the distance between the points A(a,b) to B(c,d) is $\mathbf{d} =\sqrt{\left( a-c\right)^{2} +\left( b-d\right)^{2} }$ ............(1)
Complete step-by-step solution:
Now by the above formula we can find the distance between Q(0,1) and P(5,-3),
QP$$=\sqrt{\left( 0-5\right)^{2} +\left( 1-\left( -3\right) \right)^{2} }$$
$$=\sqrt{\left( -5\right)^{2} +\left( 1+3\right)^{2} }$$
$$=\sqrt{25+4^{2}}$$
$$=\sqrt{25+16}$$
$$=\sqrt{41}$$
And the distance between Q(0,1) and R(x,6),
QR$$=\sqrt{\left( 0-x\right)^{2} +\left( 1-6\right)^{2} }$$
$$=\sqrt{x^{2}+\left( -5\right)^{2} }$$
$$=\sqrt{x^{2}+25}$$
Now since, the distance between the QP and QR are equal, then we can write,
QP = QR
$$\Rightarrow \sqrt{41} =\sqrt{x^{2}+25}$$
$$\Rightarrow \sqrt{x^{2}+25} =\sqrt{41}$$
$$\Rightarrow \left( \sqrt{x^{2}+25} \right) =\left( \sqrt{41} \right)^{2}$$ [squaring both side]
$$\Rightarrow x^{2}+25=41$$
$$\Rightarrow x^{2}=41-25$$
$$\Rightarrow x^{2}=16$$
$$\Rightarrow x=\pm \sqrt{16}$$
$$\Rightarrow x=\pm 4$$
Therefore, the coordinate of R is either (4,6) or (-4,6)
Now, when R=(4,6)
QR=$$\sqrt{\left( 0-4\right)^{2} +\left( 1-6\right)^{2} }$$
=$$\sqrt{16+25} =\sqrt{41}$$
Similarly when R=(-4,6) then
QR=$$\sqrt{\left( 0+4\right)^{2} +\left( 1-6\right)^{2} }$$
=$$\sqrt{16+25} =\sqrt{41}$$
Now when R=(4,6)
$$PR=\sqrt{\left( 5-4\right)^{2} +\left( -3-6\right)^{2} }$$
$$=\sqrt{1+\left( -9\right)^{2} } =\sqrt{1+81} =\sqrt{82}$$
And when R=(-4,6) then
PR$$=\sqrt{\left( 5-\left( -4\right) \right)^{2} +\left( -3-6\right)^{2} } =\sqrt{9^{2}+9^{2}}$$
=$$\sqrt{81+81}$$=$$\sqrt{162}$$
Therefore we can say that the coordinate of R is (4,6) or (-4,6) and QR=$\sqrt{41}$ and PR=$\sqrt{82}$ or $\sqrt{162}$ .
Note: While solving we got two coordinates for R, so why do we get two points? It is because in the first condition it is given that from point Q the distance of P and R are the same so there might be more than one point(point R) whose distance is equal to QP.
So you can understand it by a simple diagram,
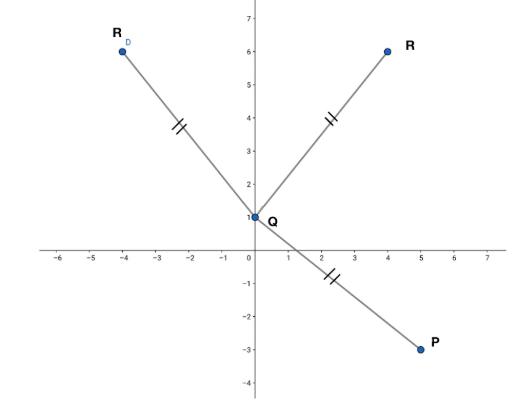
Complete step-by-step solution:
Now by the above formula we can find the distance between Q(0,1) and P(5,-3),
QP$$=\sqrt{\left( 0-5\right)^{2} +\left( 1-\left( -3\right) \right)^{2} }$$
$$=\sqrt{\left( -5\right)^{2} +\left( 1+3\right)^{2} }$$
$$=\sqrt{25+4^{2}}$$
$$=\sqrt{25+16}$$
$$=\sqrt{41}$$
And the distance between Q(0,1) and R(x,6),
QR$$=\sqrt{\left( 0-x\right)^{2} +\left( 1-6\right)^{2} }$$
$$=\sqrt{x^{2}+\left( -5\right)^{2} }$$
$$=\sqrt{x^{2}+25}$$
Now since, the distance between the QP and QR are equal, then we can write,
QP = QR
$$\Rightarrow \sqrt{41} =\sqrt{x^{2}+25}$$
$$\Rightarrow \sqrt{x^{2}+25} =\sqrt{41}$$
$$\Rightarrow \left( \sqrt{x^{2}+25} \right) =\left( \sqrt{41} \right)^{2}$$ [squaring both side]
$$\Rightarrow x^{2}+25=41$$
$$\Rightarrow x^{2}=41-25$$
$$\Rightarrow x^{2}=16$$
$$\Rightarrow x=\pm \sqrt{16}$$
$$\Rightarrow x=\pm 4$$
Therefore, the coordinate of R is either (4,6) or (-4,6)
Now, when R=(4,6)
QR=$$\sqrt{\left( 0-4\right)^{2} +\left( 1-6\right)^{2} }$$
=$$\sqrt{16+25} =\sqrt{41}$$
Similarly when R=(-4,6) then
QR=$$\sqrt{\left( 0+4\right)^{2} +\left( 1-6\right)^{2} }$$
=$$\sqrt{16+25} =\sqrt{41}$$
Now when R=(4,6)
$$PR=\sqrt{\left( 5-4\right)^{2} +\left( -3-6\right)^{2} }$$
$$=\sqrt{1+\left( -9\right)^{2} } =\sqrt{1+81} =\sqrt{82}$$
And when R=(-4,6) then
PR$$=\sqrt{\left( 5-\left( -4\right) \right)^{2} +\left( -3-6\right)^{2} } =\sqrt{9^{2}+9^{2}}$$
=$$\sqrt{81+81}$$=$$\sqrt{162}$$
Therefore we can say that the coordinate of R is (4,6) or (-4,6) and QR=$\sqrt{41}$ and PR=$\sqrt{82}$ or $\sqrt{162}$ .
Note: While solving we got two coordinates for R, so why do we get two points? It is because in the first condition it is given that from point Q the distance of P and R are the same so there might be more than one point(point R) whose distance is equal to QP.
So you can understand it by a simple diagram,

Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

The largest wind power cluster is located in the state class 11 social science CBSE

Explain zero factorial class 11 maths CBSE

State and prove Bernoullis theorem class 11 physics CBSE

What steps did the French revolutionaries take to create class 11 social science CBSE

Which among the following are examples of coming together class 11 social science CBSE




