Question

If P,Q are two points on the line \[3x+4y+15=0\] such that \[OP=OQ=9\], then the area of \[\Delta OPQ\]?
\[\begin{align}
  & A)6\sqrt{2} \\
 & B)9\sqrt{2} \\
 & C)12\sqrt{2} \\
 & D)18\sqrt{2} \\
\end{align}\]

Answer 1

Hint: First of all, we have to understand the concept of Pythagoras theorem. We should be aware of the concept of finding the perpendicular distance from (0,0) to the line \[ax+by+c=0\]. We can find the perpendicular distance from (0,0) to the line \[ax+by+c=0\] by using the formula $\dfrac{|c|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$. We know that the area of the triangle is equal to half of the product of base and height. By using these concepts, we can find the area of \[\Delta OPQ\].

Complete step-by-step solution:
Before solving the question, we should know the concept of the Pythagoras theorem. We should be aware of the concept of finding the perpendicular distance from (0,0) to the line \[ax+by+c=0\]. Let us assume C as the midpoint of PQ and find the distance using the formula: $\dfrac{|c|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$.Then derive the value of PQ using the Pythagoras theorem. As we know the area of \[\Delta OPQ=\dfrac{1}{2}\left( OC \right)\left( PQ \right)\]. Then calculate the area of the △OPQ using the PQ and OC values.

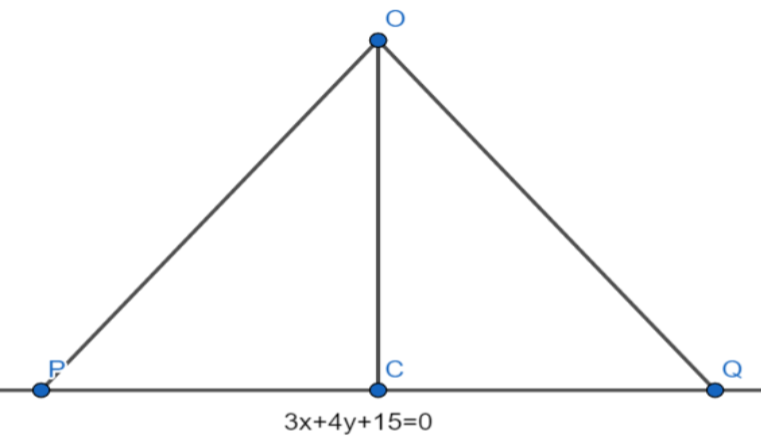
From the question we have,
OP=OQ=9,
This implies that △OPQ is an isosceles triangle.
The length of OC is equal to length of the perpendicular from (0,0) to the line 3x+4y+15=0
 $\begin{align}
  & \Rightarrow OC=\dfrac{15}{\sqrt{{{3}^{2}}+{{4}^{2}}}} \\
 & \Rightarrow OC=\dfrac{15}{\sqrt{9+16}} \\
 & \Rightarrow OC=\dfrac{15}{\sqrt{25}} \\
 & \Rightarrow OC=\dfrac{15}{5} \\
 & \Rightarrow OC=3 \\
\end{align}$

In the right-angled triangle △OCP, by Pythagoras theorem
 \[\begin{align}
  & \Rightarrow O{{P}^{2}}=P{{C}^{2}}+O{{C}^{2}} \\
 & \Rightarrow {{9}^{2}}={{3}^{2}}+P{{C}^{2}} \\
 & \Rightarrow 81=9+P{{C}^{2}} \\
 & \Rightarrow P{{C}^{2}}=72 \\
 & \Rightarrow PC=6\sqrt{2} \\
\end{align}\]
As C is the midpoint of PQ.
\[\begin{align}
  & \Rightarrow PQ=2\left( 6\sqrt{2} \right) \\
 & \Rightarrow PQ=12\sqrt{2} \\
\end{align}\]
We know that area of triangle \[\Delta OPQ=\dfrac{1}{2}\left( OC \right)\left( PQ \right)=\dfrac{1}{2}\left( 3 \right)\left( 12\sqrt{2} \right)=18\sqrt{2}\]
Hence, option (D) is correct.

Note: Students should able to illustrate the diagram in a proper manner. If the diagram drawn is incorrect, then we cannot get the correct answer. So, a diagram is necessary for such questions. Students should have a clear view of the calculation. If a small mistake is done, then the solution goes on wrong. So, the calculation should be done in a careful manner.